Advertisements
Advertisements
Question
A graph representing the function f(x) is given in it is clear that f(9) = 2
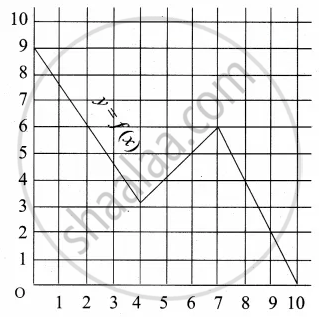
Describe the following Domain
Solution
Domain = {0, 1, 2, 3, …, 10}
= {x / 0 ≤ x ≤ 10, x ∈ R}
APPEARS IN
RELATED QUESTIONS
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(viii) \[\frac{5}{8}\]
If f is a real function satisfying \[f\left( x + \frac{1}{x} \right) = x^2 + \frac{1}{x^2}\]
for all x ∈ R − {0}, then write the expression for f(x).
If f : [−2, 2] → R is defined by \[f\left( x \right) = \begin{cases}- 1, & \text{ for } - 2 \leq x \leq 0 \\ x - 1, & \text{ for } 0 \leq x \leq 2\end{cases}\] , then
{x ∈ [−2, 2] : x ≤ 0 and f (|x|) = x} =
Find the domain and range of the following function.
f(x) = 7x2 + 4x − 1
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range.
{(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
The domain of the function f defined by f(x) = `1/sqrt(x - |x|)` is ______.
The domain and range of real function f defined by f(x) = `sqrt(x - 1)` is given by ______.
If f: R `rightarrow` R be a function defined by f(x) = 4x3 – 7. Then ______.
lf f : [0, ∞) `rightarrow` [0, ∞) and f(x) = `x/(1 + x)`, then f is ______.
The range of the function f(x) = `""^(7 - x)P_(x - 3)` is ______.
