Advertisements
Advertisements
Question
If f(m) = m2 − 3m + 1, find f(−3)
Solution
f(–3) = (–3)2 – 3(–3) + 1
= 9 + 9 + 1 = 19
APPEARS IN
RELATED QUESTIONS
A function f : R → R is defined by f(x) = x2. Determine (a) range of f, (b) {x : f(x) = 4}, (c) [y: f(y) = −1].
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iii) \[\frac{f}{g}\]
If f(x) = sin [π2] x + sin [−π]2 x, where [x] denotes the greatest integer less than or equal to x, then
The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is
The domain of the function \[f\left( x \right) = \sqrt{5 \left| x \right| - x^2 - 6}\] is
If f(m) = m2 − 3m + 1, find f(0)
Find the domain and range of the following function.
f(x) = 7x2 + 4x − 1
Find the domain of f(x) = ln (x − 5)
Write the following expression as sum or difference of logarithm
`log (sqrt(x) root(3)(y))`
If x = loga bc, y = logb ca, z = logc ab then prove that `1/(1 + x) + 1/(1 + y) + 1/(1 + z)` = 1
If f(x) = 3x + 5, g(x) = 6x − 1, then find (fg) (3)
Answer the following:
If f(x) = 3x4 – 5x2 + 7 find f(x – 1)
Answer the following:
If `log"a"/(x + y - 2z) = log"b"/(y + z - 2x) = log"c"/(z + x - 2y)`, show that abc = 1
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - x^2) + sqrt(5 - x)`
A graph representing the function f(x) is given in it is clear that f(9) = 2
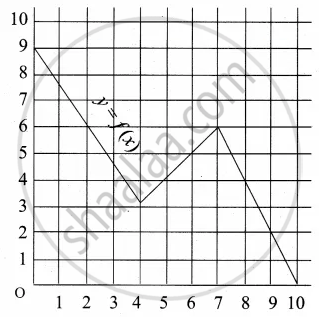
Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
If a function f(x) is given as f(x) = x2 – 6x + 4 for all x ∈ R, then f(–3) = ______.
Find the domain of the following function.
f(x) = `x/(x^2 + 3x + 2)`
The ratio `(2^(log_2 1/4 a) - 3^(log_27(a^2 + 1)^3) - 2a)/(7^(4log_49a) - a - 1)` simplifies to ______.
lf f : [0, ∞) `rightarrow` [0, ∞) and f(x) = `x/(1 + x)`, then f is ______.
Range of the function f(x) = `x/(1 + x^2)` is ______.
