Advertisements
Advertisements
प्रश्न
If `log(( x - y)/4) = logsqrt(x) + log sqrt(y)`, show that (x + y)2 = 20xy
उत्तर
`log(( x - y)/4) = logsqrt(x) + log sqrt(y)`
∴ `log((x - y)/4) = log(sqrt(x) sqrt(y))` ...[log m + log n = log mn]
∴ `log((x - y)/4) = logsqrt(xy)`
∴ `(x - y)/4 = sqrt(xy)`
Squaring on both sides, we get
`(x - y)^2/16` = xy
∴ x2 – 2xy + y2 = 16xy
Adding 4xy on both sides, we get
x2 + 2xy + y2 = 20xy
∴ (x + y)2 = 20xy
APPEARS IN
संबंधित प्रश्न
Define a function as a correspondence between two sets.
Let f : R+ → R, where R+ is the set of all positive real numbers, such that f(x) = loge x. Determine
(c) whether f(xy) = f(x) : f(y) holds
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(viii) \[\frac{5}{8}\]
Write the range of the function f(x) = cos [x], where \[\frac{- \pi}{2} < x < \frac{\pi}{2}\] .
Write the domain and range of function f(x) given by \[f\left( x \right) = \sqrt{\left[ x \right] - x}\] .
Let f and g be two functions given by
f = {(2, 4), (5, 6), (8, −1), (10, −3)} and g = {(2, 5), (7, 1), (8, 4), (10, 13), (11, −5)}.
Find the domain of f + g
Find the set of values of x for which the functions f(x) = 3x2 − 1 and g(x) = 3 + x are equal.
The range of f(x) = cos [x], for π/2 < x < π/2 is
If 2f (x) − \[3f\left( \frac{1}{x} \right) = x^2\] (x ≠ 0), then f(2) is equal to
If \[e^{f\left( x \right)} = \frac{10 + x}{10 - x}\] , x ∈ (−10, 10) and \[f\left( x \right) = kf\left( \frac{200 x}{100 + x^2} \right)\] , then k =
If f : R → R be given by for all \[f\left( x \right) = \frac{4^x}{4^x + 2}\] x ∈ R, then
The domain of the function
The domain of definition of \[f\left( x \right) = \sqrt{\frac{x + 3}{\left( 2 - x \right) \left( x - 5 \right)}}\] is
The domain of definition of \[f\left( x \right) = \sqrt{x - 3 - 2\sqrt{x - 4}} - \sqrt{x - 3 + 2\sqrt{x - 4}}\] is
The range of the function f(x) = |x − 1| is
Express the area A of a square as a function of its side s
lf f(x) = 3(4x+1), find f(– 3)
Answer the following:
Let f : R → R be given by f(x) = x + 5 for all x ∈ R. Draw its graph
Answer the following:
For any base show that log (1 + 2 + 3) = log 1 + log 2 + log 3
Answer the following:
If `log (("a" + "b")/2) = 1/2(log"a" + log"b")`, then show that a = b
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - 3) + 1/(log(5 - x))`
Given the function f: x → x2 – 5x + 6, evaluate f(2)
A graph representing the function f(x) is given in it is clear that f(9) = 2
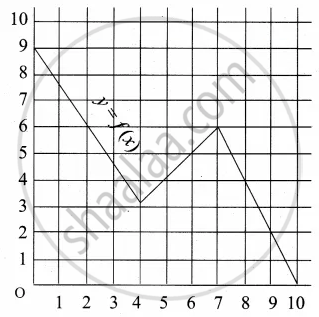
Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
A function f is defined by f(x) = 2x – 3 find x such that f(x) = x
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Calculate the value of `"gg" (1/2)`
The range of 7, 11, 16, 27, 31, 33, 42, 49 is ______.
The domain of the real valued function f(x) = `sqrt((x - 2)/(3 - x))` is ______.
Mapping f: R → R which is defined as f(x) = sin x, x ∈ R will be ______
If a function f(x) is given as f(x) = x2 – 6x + 4 for all x ∈ R, then f(–3) = ______.
The domain of the function f(x) = log3+x (x2 - 1) is ______.
Domain of function f(x) = cos–1 6x is ______.
Find the domain of the following function.
f(x) = [x] + x
Find the range of the following functions given by `|x - 4|/(x - 4)`
Find the domain of the function f given by f(x) = `1/sqrt([x]^2 - [x] - 6)`
Find the domain of the following functions given by f(x) = x|x|
Find the range of the following functions given by f(x) = 1 + 3 cos2x
(Hint: –1 ≤ cos 2x ≤ 1 ⇒ –3 ≤ 3 cos 2x ≤ 3 ⇒ –2 ≤ 1 + 3cos 2x ≤ 4)
The domain for which the functions defined by f(x) = 3x2 – 1 and g(x) = 3 + x are equal is ______.
If f: R `rightarrow` R be a function defined by f(x) = 4x3 – 7. Then ______.
The range of the function f(x) = `""^(7 - x)P_(x - 3)` is ______.
