Advertisements
Advertisements
प्रश्न
Find the domain and range of the following function.
f(x) = `root(3)(x + 1)`
उत्तर
f(x) = `root(3)(x + 1)`
f(x) is defined for all x ∈ R
∴ Domain = R
If y = `root(3)(x + 1)`, y can take any real value
∴ Range = R
∴ Domain = Range = R.
APPEARS IN
संबंधित प्रश्न
Let A = {−2, −1, 0, 1, 2} and f : A → Z be a function defined by f(x) = x2 − 2x − 3. Find:
(a) range of f, i.e. f(A).
Let f : R+ → R, where R+ is the set of all positive real numbers, such that f(x) = loge x. Determine
(a) the image set of the domain of f
If \[f\left( x \right) = \begin{cases}x^2 , & \text{ when } x < 0 \\ x, & \text{ when } 0 \leq x < 1 \\ \frac{1}{x}, & \text{ when } x \geq 1\end{cases}\]
find: (a) f(1/2), (b) f(−2), (c) f(1), (d)
If f(x) = (a − xn)1/n, a > 0 and n ∈ N, then prove that f(f(x)) = x for all x.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(i) f + g
Let f : [0, ∞) → R and g : R → R be defined by \[f\left( x \right) = \sqrt{x}\] and g(x) = x. Find f + g, f − g, fg and \[\frac{f}{g}\] .
Let \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] . Then write the value of α satisfying f(f(x)) = x for all x ≠ −1.
If \[f\left( x \right) = \frac{\sin^4 x + \cos^2 x}{\sin^2 x + \cos^4 x}\] for x ∈ R, then f (2002) =
If f : [−2, 2] → R is defined by \[f\left( x \right) = \begin{cases}- 1, & \text{ for } - 2 \leq x \leq 0 \\ x - 1, & \text{ for } 0 \leq x \leq 2\end{cases}\] , then
{x ∈ [−2, 2] : x ≤ 0 and f (|x|) = x} =
The domain of the function \[f\left( x \right) = \sqrt{5 \left| x \right| - x^2 - 6}\] is
If f(m) = m2 − 3m + 1, find f(0)
If f(m) = m2 − 3m + 1, find f(− x)
If f(x) =` (2x−1)/ (5x−2) , x ≠ 2/5` Verify whether (fof) (x) = x
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 3), (4, 1), (2, 2)}
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x2
Show that if f : A → B and g : B → C are onto, then g ° f is also onto
Express the following exponential equation in logarithmic form
e–x = 6
Express the following logarithmic equation in exponential form
ln e = 1
Find the domain of f(x) = ln (x − 5)
Write the following expression as sum or difference of logarithm
`log ("pq"/"rs")`
Prove that logbm a = `1/"m" log_"b""a"`
Select the correct answer from given alternatives.
Find x, if 2log2 x = 4
Select the correct answer from given alternatives
If f(x) = 2x2 + bx + c and f(0) = 3 and f(2) = 1, then f(1) is equal to
Answer the following:
Find whether the following function is one-one
f : R − {3} → R defined by f(x) = `(5x + 7)/(x - 3)` for x ∈ R − {3}
A function f is defined as : f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 3
Answer the following:
Show that, `log ("a"^2/"bc") + log ("b"^2/"ca") + log ("c"^2/"ab")` = 0
Answer the following:
If `log (("a" + "b")/2) = 1/2(log"a" + log"b")`, then show that a = b
Answer the following:
If a2 + b2 = 7ab, show that, `log(("a" + "b")/3) = 1/2 log "a" + 1/2 log "b"`
Answer the following:
Find the domain of the following function.
f(x) = `(x^2 + 4x + 4)/(x^2 + x - 6)`
A graph representing the function f(x) is given in it is clear that f(9) = 2
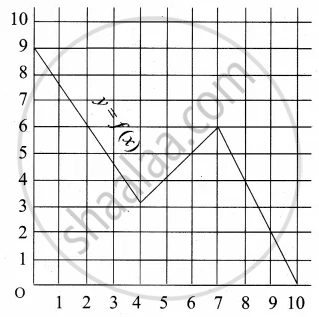
Describe the following Range
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Calculate the value of `"gg" (1/2)`
If f(x) = `1/sqrt(4 - 3x)`, then dom(f) = ______..
Find the domain of the following functions given by f(x) = `(x^3 - x + 3)/(x^2 - 1)`
Find the range of the following functions given by f(x) = `3/(2 - x^2)`
Find the range of the following functions given by f(x) = 1 – |x – 2|
Find the domain and range of the function f(x) = `1/sqrt(x - 5)`
The domain and range of the function f given by f(x) = 2 – |x – 5| is ______.
