Advertisements
Advertisements
प्रश्न
The domain of the function f defined by f(x) = `1/sqrt(x - |x|)` is ______.
विकल्प
R
R+
R–
None of these
उत्तर
none of these
Explanation:
Given that f(x) = `1/sqrt(x - |x|)`
Where `x - |x| = {{:(x - x = 0, "if" x ≥ 0),(2x, "if" x < 0):}`
Thus `1/sqrt(x - |x|)` is not defined for any x ∈ R.
Hence f is not defined for any x ∈ R.
APPEARS IN
संबंधित प्रश्न
What is the fundamental difference between a relation and a function? Is every relation a function?
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
(c) f3 = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
The function f is defined by \[f\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 3 \\ 3x, & 3 \leq x \leq 10\end{cases}\]
The relation g is defined by \[g\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 2 \\ 3x, & 2 \leq x \leq 10\end{cases}\]
Show that f is a function and g is not a function.
If f, g and h are real functions defined by
If f is a real function satisfying \[f\left( x + \frac{1}{x} \right) = x^2 + \frac{1}{x^2}\]
for all x ∈ R − {0}, then write the expression for f(x).
If f, g, h are real functions given by f(x) = x2, g(x) = tan x and h(x) = loge x, then write the value of (hogof)\[\left( \sqrt{\frac{\pi}{4}} \right)\] .
Write the domain and range of function f(x) given by
If \[f\left( x \right) = \frac{2^x + 2^{- x}}{2}\] , then f(x + y) f(x − y) is equal to
Check if the following relation is a function.
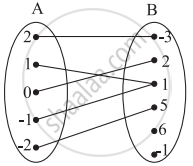
Check if the relation given by the equation represents y as function of x:
2y + 10 = 0
If f(m) = m2 − 3m + 1, find f(− x)
If f(m) = m2 − 3m + 1, find `(("f"(2 + "h") - "f"(2))/"h"), "h" ≠ 0`
Find x, if f(x) = g(x) where f(x) = `sqrt(x) - 3`, g(x) = 5 – x
Express the area A of circle as a function of its circumference C.
An open box is made from a square of cardboard of 30 cms side, by cutting squares of length x centimeters from each corner and folding the sides up. Express the volume of the box as a function of x. Also find its domain
Express the following exponential equation in logarithmic form
e–x = 6
Express the following logarithmic equation in exponential form
ln e = 1
If `log((x + y)/3) = 1/2 log x + 1/2 logy`, show that `x/y + y/x` = 7
If f(x) = 3x + 5, g(x) = 6x − 1, then find `("f"/"g") (x)` and its domain
Select the correct answer from given alternatives.
If f(x) =`1/(1 - x)`, then f{f[f(x)]} is
Select the correct answer from given alternatives
If f(x) = 2x2 + bx + c and f(0) = 3 and f(2) = 1, then f(1) is equal to
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range
{(12, 1), (3, 1), (5, 2)}
Answer the following:
If f(x) = 3x + a and f(1) = 7 find a and f(4)
Answer the following:
Let f : R – {2} → R be defined by f(x) = `(x^2 - 4)/(x - 2)` and g : R → R be defined by g(x) = x + 2. Examine whether f = g or not
Answer the following:
Without using log tables, prove that `2/5 < log_10 3 < 1/2`
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - 3) + 1/(log(5 - x))`
Find the range of the following functions given by `|x - 4|/(x - 4)`
If f(x) = `(x - 1)/(x + 1)`, then show that `f(1/x)` = – f(x)
The range of the function f(x) = x2 + 2x+ 2 is ______.
