Advertisements
Advertisements
प्रश्न
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
विकल्प
(a) {−1, 1}
(b) {−1, 0, 1}
(c) {1}
(d) (0, ∞)
उत्तर
(a) {−1, 1}
\[\text{ For } \left| x + 2 \right| > 0, \]
\[\text{ or } x > - 2 , \]
\[y = \frac{x + 2}{x + 2} = 1\]
\[\text{ For } \left| x + 2 \right| < 0, \]
\[\text{ or } x < - 2, \]
\[y = \frac{x + 2}{- (x + 2)} = - 1\]
\[\text{ Thus } , y = { - 1, 1}\]
\[\text{ or range } f(x) = { - 1, 1} .\]
APPEARS IN
संबंधित प्रश्न
A function f : R → R is defined by f(x) = x2. Determine (a) range of f, (b) {x : f(x) = 4}, (c) [y: f(y) = −1].
If f(x) = (x − a)2 (x − b)2, find f(a + b).
If \[y = f\left( x \right) = \frac{ax - b}{bx - a}\] , show that x = f(y).
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iii) \[\frac{f}{g}\]
If f is a real function satisfying \[f\left( x + \frac{1}{x} \right) = x^2 + \frac{1}{x^2}\]
for all x ∈ R − {0}, then write the expression for f(x).
If f(x) = cos [π2]x + cos [−π2] x, where [x] denotes the greatest integer less than or equal to x, then write the value of f(π).
Write the domain and range of function f(x) given by
Write the domain and range of function f(x) given by \[f\left( x \right) = \sqrt{\left[ x \right] - x}\] .
Which one of the following is not a function?
If \[f\left( x \right) = \frac{2^x + 2^{- x}}{2}\] , then f(x + y) f(x − y) is equal to
Let f : R → R be defined by f(x) = 2x + |x|. Then f(2x) + f(−x) − f(x) =
The domain of definition of the function f(x) = log |x| is
Check if the relation given by the equation represents y as function of x:
x2 − y = 25
Find x, if g(x) = 0 where g(x) = `(18 -2x^2)/7`
Express the area A of circle as a function of its radius r
Express the following exponential equation in logarithmic form
54° = 1
Express the following exponential equation in logarithmic form
`9^(3/2)` = 27
Express the following logarithmic equation in exponential form
`log_5 1/25` = – 2
Select the correct answer from given alternatives.
If f(x) =`1/(1 - x)`, then f{f[f(x)]} is
Select the correct answer from given alternatives.
If f : R → R is defined by f(x) = x3 then f–1 (8) is equal to :
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range.
{(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range.
{(0, 0), (1, 1), (1, –1), (4, 2), (4, –2), (9, 3), (9, –3), (16, 4), (16, –4)}
Answer the following:
Find whether the following function is one-one
f : R − {3} → R defined by f(x) = `(5x + 7)/(x - 3)` for x ∈ R − {3}
Answer the following:
A function f is defined as : f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 5
Answer the following:
Find the domain of the following function.
f(x) = `(x^2 + 4x + 4)/(x^2 + x - 6)`
A graph representing the function f(x) is given in it is clear that f(9) = 2
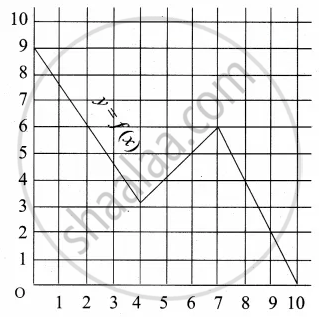
Describe the following Domain
A graph representing the function f(x) is given in it is clear that f(9) = 2
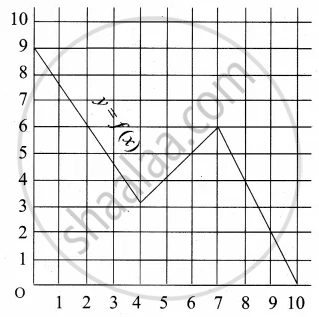
Describe the following Range
If the domain of function f(a) = a2 - 4a + 8 is (-∞, ∞), then the range of function is ______
Find the range of the following functions given by `sqrt(16 - x^2)`
Redefine the function which is given by f(x) = `|x - 1| + |1 + x|, -2 ≤ x ≤ 2`
Let A and B be any two sets such that n(B) = p, n(A) = q then the total number of functions f : A → B is equal to ______.
Find the domain of the following functions given by f(x) = x|x|
Find the range of the following functions given by f(x) = 1 – |x – 2|
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f – g)(x)
Let f(x) and g(x) be two real polynomials of degree 2 and 1 respectively. If f(g(x)) = 8x2 – 2x, and g(f(x)) = 4x2 + 6x + 1, then the value of f(2) + g(2) is ______.
If f(x) = x3 – 1 and domain of f = {0, 1, 2, 3}, then domain of f–1 is ______.
