Advertisements
Advertisements
प्रश्न
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iii) \[\frac{f}{g}\]
उत्तर
Given:
f(x) = loge (1 − x) and g(x) = [x]
Clearly, f(x) = loge (1 − x) is defined for all ( 1 -x) > 0.
⇒ 1 > x
⇒ x < 1
⇒ x ∈ ( -∞, 1)
Thus, domain (f ) = ( - ∞, 1)
Again,
g(x) = [x] is defined for all x ∈ R.
Thus, domain (g) = R
∴ Domain (f) ∩ Domain (g) = ( - ∞, 1) ∩ R = ( -∞, 1)
Hence,
(iii) Given:
g(x) = [ x ]
If [ x ] = 0,
x ∈ (0, 1)
Thus,
APPEARS IN
संबंधित प्रश्न
Define a function as a correspondence between two sets.
find: f(1), f(−1), f(0) and f(2).
If f : R → R be defined by f(x) = x2 + 1, then find f−1 [17] and f−1 [−3].
If \[f\left( x \right) = \frac{1}{1 - x}\] , show that f[f[f(x)]] = x.
If \[f\left( x \right) = \begin{cases}x^2 , & \text{ when } x < 0 \\ x, & \text{ when } 0 \leq x < 1 \\ \frac{1}{x}, & \text{ when } x \geq 1\end{cases}\]
find: (a) f(1/2), (b) f(−2), (c) f(1), (d)
Write the domain and range of the function \[f\left( x \right) = \frac{x - 2}{2 - x}\] .
The range of f(x) = cos [x], for π/2 < x < π/2 is
If \[f\left( x \right) = \log \left( \frac{1 + x}{1 - x} \right) \text{ and} g\left( x \right) = \frac{3x + x^3}{1 + 3 x^2}\] , then f(g(x)) is equal to
Let f(x) = x, \[g\left( x \right) = \frac{1}{x}\] and h(x) = f(x) g(x). Then, h(x) = 1
If \[3f\left( x \right) + 5f\left( \frac{1}{x} \right) = \frac{1}{x} - 3\] for all non-zero x, then f(x) =
The domain of the function
The domain of definition of \[f\left( x \right) = \sqrt{\frac{x + 3}{\left( 2 - x \right) \left( x - 5 \right)}}\] is
The domain of definition of the function \[f\left( x \right) = \sqrt{x - 1} + \sqrt{3 - x}\] is
If f(x) =` (2x−1)/ (5x−2) , x ≠ 2/5` Verify whether (fof) (x) = x
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 1), (2, 1), (3, 1), (4, 1)}
If f(m) = m2 − 3m + 1, find f(−3)
If f(m) = m2 − 3m + 1, find f(x + 1)
lf f(x) = 3(4x+1), find f(– 3)
Express the following logarithmic equation in exponential form
`log_5 1/25` = – 2
Write the following expression as sum or difference of logarithm
`log ("pq"/"rs")`
Write the following expression as sum or difference of logarithm
In `(("a"^3 ("a" - 2)^2)/sqrt("b"^2 + 5))`
If f(x) = ax2 − bx + 6 and f(2) = 3 and f(4) = 30, find a and b
Answer the following:
Let f: R → R be a function defined by f(x) = 5x3 – 8 for all x ∈ R, show that f is one-one and onto. Hence find f –1
Answer the following:
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
If b2 = ac. prove that, log a + log c = 2 log b
Answer the following:
Solve for x, logx (8x – 3) – logx 4 = 2
Answer the following:
If `log ((x - y)/5) = 1/2 logx + 1/2 log y`, show that x2 + y2 = 27xy
Answer the following:
Show that, logy x3 . logz y4 . logx z5 = 60
Answer the following:
If `log_2"a"/4 = log_2"b"/6 = log_2"c"/(3"k")` and a3b2c = 1 find the value of k
Answer the following:
Find the range of the following function.
f(x) = 1 + 2x + 4x
A function f is defined by f(x) = 2x – 3 find x such that f(x) = 0
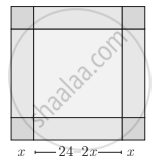
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal square from the corner and turning up the side as shown. Express the volume V of the box as a function of x
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Calculate the value of `"gg" (1/2)`
Redefine the function which is given by f(x) = `|x - 1| + |1 + x|, -2 ≤ x ≤ 2`
If f(x) = `(x - 1)/(x + 1)`, then show that `f(- 1/x) = (-1)/(f(x))`
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f – g)(x)
The domain of the function f given by f(x) = `(x^2 + 2x + 1)/(x^2 - x - 6)` is ______.
