Advertisements
Advertisements
प्रश्न
Write the domain and range of the function \[f\left( x \right) = \frac{x - 2}{2 - x}\] .
उत्तर
Given: \[f\left( x \right) = \frac{x - 2}{2 - x}\] Domain ( f ) :
Clearly, f (x) is defined for all x satisfying: if 2 -x ≠ 0 ⇒ x ≠ 2.
Hence, domain ( f ) = R -{2}
Range of f :
Let f (x) = y
⇒ \[\frac{x - 2}{2 - x} = y\]
⇒ x - 2 = y (2 -x)
⇒ x -2 = - y (x -2)
⇒ y = -1
Hence, range ( f ) = { -1}.
APPEARS IN
संबंधित प्रश्न
The function f is defined by \[f\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 3 \\ 3x, & 3 \leq x \leq 10\end{cases}\]
The relation g is defined by \[g\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 2 \\ 3x, & 2 \leq x \leq 10\end{cases}\]
Show that f is a function and g is not a function.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iii) f g
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iv) \[\frac{f}{g}\]
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(v) \[\frac{g}{f}\]
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(ii) fg
Write the range of the function f(x) = cos [x], where \[\frac{- \pi}{2} < x < \frac{\pi}{2}\] .
The range of the function \[f\left( x \right) = \frac{x^2 - x}{x^2 + 2x}\] is
The domain of definition of the function \[f\left( x \right) = \sqrt{x - 1} + \sqrt{3 - x}\] is
The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is
The domain of the function \[f\left( x \right) = \sqrt{5 \left| x \right| - x^2 - 6}\] is
Check if the following relation is function:

If f(m) = m2 − 3m + 1, find `f(1/2)`
Which of the following relations are functions? If it is a function determine its domain and range:
{(1, 1), (3, 1), (5, 2)}
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(2)
Check if the following relation is a function.
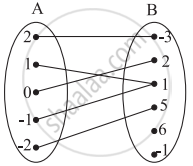
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 0), (3, 3), (2, −1), (4, 1), (2, 2)}
Find x, if g(x) = 0 where g(x) = `(18 -2x^2)/7`
Find the domain and range of the following function.
f(x) = `sqrt((x - 3)/(7 - x))`
Express the area A of circle as a function of its circumference C.
If `log((x + y)/3) = 1/2 log x + 1/2 logy`, show that `x/y + y/x` = 7
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f − g) (2)
Select the correct answer from given alternatives.
If log10(log10(log10x)) = 0 then x =
Select the correct answer from given alternatives
The domain of `1/([x] - x)` where [x] is greatest integer function is
Answer the following:
For any base show that log (1 + 2 + 3) = log 1 + log 2 + log 3
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - 3) + 1/(log(5 - x))`
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - x^2) + sqrt(5 - x)`
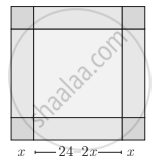
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal square from the corner and turning up the side as shown. Express the volume V of the box as a function of x
A function f is defined by f(x) = 3 – 2x. Find x such that f(x2) = (f(x))2
The data in the adjacent table depicts the length of a person's forehand and their corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length (x) as y = ax + b, where a, b are constant.
| Length ‘x’ of forehand (in cm) |
Height 'y' (in inches) |
| 35 | 56 |
| 45 | 65 |
| 50 | 69.5 |
| 55 | 74 |
Check if this relation is a function
If f(x) = 5x - 3, then f-1(x) is ______
The domain of the real valued function f(x) = `sqrt((x - 2)/(3 - x))` is ______.
Find the domain of the following function.
f(x) = `x/(x^2 + 3x + 2)`
Find the domain of the following functions given by f(x) = `(x^3 - x + 3)/(x^2 - 1)`
Let f(x) = `sqrt(1 + x^2)`, then ______.
The domain and range of real function f defined by f(x) = `sqrt(x - 1)` is given by ______.
Which of the following functions is NOT one-one?
Let f(θ) = sin θ (sin θ + sin 3θ) then ______.
