Advertisements
Advertisements
प्रश्न
The range of the function \[f\left( x \right) = \frac{x^2 - x}{x^2 + 2x}\] is
विकल्प
(a) R
(b) R − {1}
(c) R − {−1/2, 1}
(d) None of these
उत्तर
(c) R − {−1/2, 1}
\[ \Rightarrow y = \frac{x(x - 1)}{x(x + 2)}\]
\[ \Rightarrow y = \frac{(x - 1)}{(x + 2)}\]
\[ \Rightarrow xy + 2y = x - 1\]
\[ \Rightarrow x = \frac{2y + 1}{1 - y}\]
\[\text{ Here } , 1 - y \neq 0 . \]
\[\text{ or } , y \neq 1 . \]
\[\text{ Also } , x \neq 0\]
\[ \Rightarrow \frac{2y + 1}{1 - y} \neq 0\]
\[ \Rightarrow y \neq - \frac{1}{2}\]
\[\text{ Thus, range } (f) = R - { - \frac{1}{2}, 1} . \]
APPEARS IN
संबंधित प्रश्न
Find the domain of the function f(x) = `(x^2 + 2x + 1)/(x^2 - 8x + 12)`
Let A = {9, 10, 11, 12, 13} and let f: A → N be defined by f(n) = the highest prime factor of n. Find the range of f.
A function f : R → R is defined by f(x) = x2. Determine (a) range of f, (b) {x : f(x) = 4}, (c) [y: f(y) = −1].
If f(x) = x2 − 3x + 4, then find the values of x satisfying the equation f(x) = f(2x + 1).
If \[f\left( x \right) = \begin{cases}x^2 , & \text{ when } x < 0 \\ x, & \text{ when } 0 \leq x < 1 \\ \frac{1}{x}, & \text{ when } x \geq 1\end{cases}\]
find: (a) f(1/2), (b) f(−2), (c) f(1), (d)
If for non-zero x, af(x) + bf \[\left( \frac{1}{x} \right) = \frac{1}{x} - 5\] , where a ≠ b, then find f(x).
Write the range of the function f(x) = cos [x], where \[\frac{- \pi}{2} < x < \frac{\pi}{2}\] .
Let f(x) = x, \[g\left( x \right) = \frac{1}{x}\] and h(x) = f(x) g(x). Then, h(x) = 1
If \[f\left( x \right) = 64 x^3 + \frac{1}{x^3}\] and α, β are the roots of \[4x + \frac{1}{x} = 3\] . Then,
The domain of definition of the function \[f\left( x \right) = \sqrt{\frac{x - 2}{x + 2}} + \sqrt{\frac{1 - x}{1 + x}}\] is
The domain of definition of \[f\left( x \right) = \sqrt{4x - x^2}\] is
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
Check if the following relation is a function.
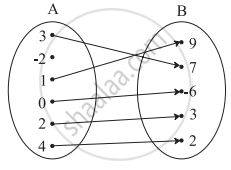
If f(m) = m2 − 3m + 1, find f(−3)
Find x, if g(x) = 0 where g(x) = `(5x - 6)/7`
Express the following exponential equation in logarithmic form
e–x = 6
Write the following expression as a single logarithm.
5 log x + 7 log y − log z
Write the following expression as a single logarithm.
ln (x + 2) + ln (x − 2) − 3 ln (x + 5)
Prove that alogcb = blogca
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f + g) (x)
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f − g) (2)
The equation logx2 16 + log2x 64 = 3 has,
Answer the following:
A function f is defined as : f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 5
Answer the following:
Let f : R → R be given by f(x) = x3 + 1 for all x ∈ R. Draw its graph
Answer the following:
If `log_2"a"/4 = log_2"b"/6 = log_2"c"/(3"k")` and a3b2c = 1 find the value of k
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - x^2) + sqrt(5 - x)`
Answer the following:
Find the range of the following function.
f(x) = |x – 5|
The range of the function f(x) = `(x^2 - 3x + 2)/(x^3 - 4x^2 + 5x - 2)` is ______
If f(x) = `1/sqrt(4 - 3x)`, then dom(f) = ______..
Redefine the function which is given by f(x) = `|x - 1| + |1 + x|, -2 ≤ x ≤ 2`
Find the domain of the following functions given by f(x) = `(x^3 - x + 3)/(x^2 - 1)`
Find the domain of the following function given by:
f(x) = `(3x)/(2x - 8)`
The domain and range of real function f defined by f(x) = `sqrt(x - 1)` is given by ______.
The domain for which the functions defined by f(x) = 3x2 – 1 and g(x) = 3 + x are equal is ______.
Let f(θ) = sin θ (sin θ + sin 3θ) then ______.
Let f be a function with domain [–3, 5] and let g(x) = | 3x + 4 |. Then, the domain of (fog) (x) is ______.
The period of the function
f(x) = `(sin 8x cos x - sin 6x cos 3x)/(cos 2x cos x - sin 3x sin 4x)` is ______.
The domain of f(x) = `sin^-1 [log_2(x/2)]` is ______.
