Advertisements
Advertisements
प्रश्न
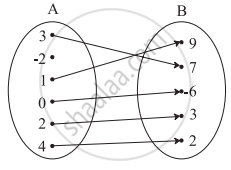
Check if the following relation is a function.
उत्तर
It is not a function because – 2 ∈ A is not related to any element of the set B.
APPEARS IN
संबंधित प्रश्न
Find the domain of the function f(x) = `(x^2 + 2x + 1)/(x^2 - 8x + 12)`
What is the fundamental difference between a relation and a function? Is every relation a function?
find: f(1), f(−1), f(0) and f(2).
Let f : R+ → R, where R+ is the set of all positive real numbers, such that f(x) = loge x. Determine
(a) the image set of the domain of f
f, g, h are three function defined from R to R as follow:
(ii) g(x) = sin x
Find the range of function.
If f(x) = (a − xn)1/n, a > 0 and n ∈ N, then prove that f(f(x)) = x for all x.
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(i) f + g
Let f : [0, ∞) → R and g : R → R be defined by \[f\left( x \right) = \sqrt{x}\] and g(x) = x. Find f + g, f − g, fg and \[\frac{f}{g}\] .
Write the range of the function f(x) = sin [x], where \[\frac{- \pi}{4} \leq x \leq \frac{\pi}{4}\] .
If f(x) = cos [π2]x + cos [−π2] x, where [x] denotes the greatest integer less than or equal to x, then write the value of f(π).
If f(x) = cos (log x), then the value of f(x) f(y) −\[\frac{1}{2}\left\{ f\left( \frac{x}{y} \right) + f\left( xy \right) \right\}\] is
Let f(x) = x, \[g\left( x \right) = \frac{1}{x}\] and h(x) = f(x) g(x). Then, h(x) = 1
The function f : R → R is defined by f(x) = cos2 x + sin4 x. Then, f(R) =
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
If \[\left[ x \right]^2 - 5\left[ x \right] + 6 = 0\], where [.] denotes the greatest integer function, then
Which of the following relations are functions? If it is a function determine its domain and range:
{(0, 0), (1, 1), (1, −1), (4, 2), (4, −2), (9, 3), (9, −3), (16, 4), (16, −4)}
Which of the following relations are functions? If it is a function determine its domain and range:
{(1, 1), (3, 1), (5, 2)}
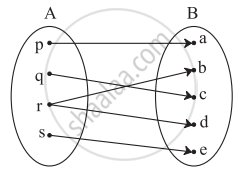
Check if the following relation is a function.
If f(m) = m2 − 3m + 1, find `f(1/2)`
Find x, if f(x) = g(x) where f(x) = x4 + 2x2, g(x) = 11x2
Write the following expression as sum or difference of logarithm
In `[(root(3)(x - 2)(2x + 1)^4)/((x + 4)sqrt(2x + 4))]^2`
Solve for x.
x + log10 (1 + 2x) = x log10 5 + log10 6
Select the correct answer from given alternatives.
If log10(log10(log10x)) = 0 then x =
Answer the following:
Find whether the following function is one-one
f : R → R defined by f(x) = x2 + 5
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
If a2 + b2 = 7ab, show that, `log(("a" + "b")/3) = 1/2 log "a" + 1/2 log "b"`
Answer the following:
Find the range of the following function.
f(x) = `x/(9 + x^2)`
Let X = {3, 4, 6, 8}. Determine whether the relation R = {(x, f(x)) | x ∈ X, f(x) = x2 + 1} is a function from X to N?
A graph representing the function f(x) is given in it is clear that f(9) = 2
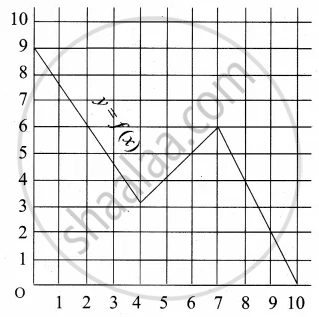
Describe the following Range
A function f is defined by f(x) = 2x – 3 find x such that f(x) = x
A function f is defined by f(x) = 3 – 2x. Find x such that f(x2) = (f(x))2
The data in the adjacent table depicts the length of a person's forehand and their corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length (x) as y = ax + b, where a, b are constant.
| Length ‘x’ of forehand (in cm) |
Height 'y' (in inches) |
| 35 | 56 |
| 45 | 65 |
| 50 | 69.5 |
| 55 | 74 |
Check if this relation is a function
A function f is defined by f(x) = 2x – 3 find x such that f(x) = f(1 – x)
The domain of the function f(x) = `sqrtx` is ______.
The function f: R `rightarrow` R defined by f(x) = sin x is ______.
Let f be a function with domain [–3, 5] and let g(x) = | 3x + 4 |. Then, the domain of (fog) (x) is ______.
