Advertisements
Advertisements
प्रश्न
Let f(x) = x, \[g\left( x \right) = \frac{1}{x}\] and h(x) = f(x) g(x). Then, h(x) = 1
विकल्प
(a) x ∈ R
(b) x ∈ Q
(c) x ∈ R − Q
(d) x ∈ R, x ≠ 0
उत्तर
(d) x ∈ R, x ≠ 0
f(x) = x, \[g\left( x \right) = \frac{1}{x}\] and h(x) = f(x) g(x) Now,
APPEARS IN
संबंधित प्रश्न
Let A = {−2, −1, 0, 1, 2} and f : A → Z be a function defined by f(x) = x2 − 2x − 3. Find:
(a) range of f, i.e. f(A).
The function f is defined by \[f\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 3 \\ 3x, & 3 \leq x \leq 10\end{cases}\]
The relation g is defined by \[g\left( x \right) = \begin{cases}x^2 , & 0 \leq x \leq 2 \\ 3x, & 2 \leq x \leq 10\end{cases}\]
Show that f is a function and g is not a function.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(viii) \[\frac{5}{8}\]
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(ii) fg
If f is a real function satisfying \[f\left( x + \frac{1}{x} \right) = x^2 + \frac{1}{x^2}\]
for all x ∈ R − {0}, then write the expression for f(x).
If\[f\left( x \right) = 1 - \frac{1}{x}\] , then write the value of \[f\left( f\left( \frac{1}{x} \right) \right)\]
Find the set of values of x for which the functions f(x) = 3x2 − 1 and g(x) = 3 + x are equal.
The range of the function \[f\left( x \right) = \frac{x}{\left| x \right|}\] is
If f(m) = m2 − 3m + 1, find f(0)
Check if the relation given by the equation represents y as function of x:
x2 − y = 25
Find x, if g(x) = 0 where g(x) = x3 − 2x2 − 5x + 6
An open box is made from a square of cardboard of 30 cms side, by cutting squares of length x centimeters from each corner and folding the sides up. Express the volume of the box as a function of x. Also find its domain
Check the injectivity and surjectivity of the following function.
f : R → R given by f(x) = x2
Express the following exponential equation in logarithmic form
10−2 = 0.01
Express the following exponential equation in logarithmic form
`"e"^(1/2)` = 1.6487
Express the following logarithmic equation in exponential form
ln e = 1
Write the following expression as a single logarithm.
5 log x + 7 log y − log z
Write the following expression as a single logarithm.
ln (x + 2) + ln (x − 2) − 3 ln (x + 5)
Prove that `"b"^(log_"b""a"` = a
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f − g) (2)
If f(x) = 3x + 5, g(x) = 6x − 1, then find (fg) (3)
Answer the following:
Solve for x, logx (8x – 3) – logx 4 = 2
Answer the following:
If `log ((x - y)/5) = 1/2 logx + 1/2 log y`, show that x2 + y2 = 27xy
Answer the following:
Solve : `sqrt(log_2 x^4) + 4log_4 sqrt(2/x)` = 2
Answer the following:
Show that, logy x3 . logz y4 . logx z5 = 60
Answer the following:
Find the range of the following function.
f(x) = |x – 5|
Answer the following:
Find (f ° g) (x) and (g ° f) (x)
f(x) = `x/(x + 1)`, g(x) = `x/(1 - x)`
A graph representing the function f(x) is given in it is clear that f(9) = 2
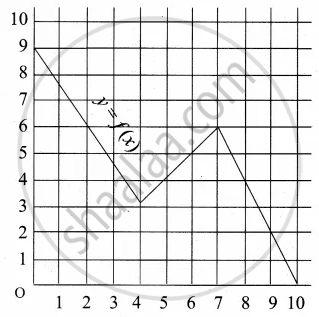
Describe the following Range
A function f is defined by f(x) = 2x – 3 find `("f"(0) + "f"(1))/2`
The range of the function f(x) = `(x^2 - 3x + 2)/(x^3 - 4x^2 + 5x - 2)` is ______
The domain of the function f(x) = log3+x (x2 - 1) is ______.
Find the range of the following functions given by f(x) = 1 – |x – 2|
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find `(f/g)(x)`
The domain and range of the real function f defined by f(x) = `(4 - x)/(x - 4)` is given by ______.
The domain of the function f(x) = `sin^-1((|x| + 5)/(x^2 + 1))` is (–∞, –a] ≈ [a, ∞). Then a is equal to ______.
