Advertisements
Advertisements
प्रश्न
A function f : R → R is defined by f(x) = x2. Determine (a) range of f, (b) {x : f(x) = 4}, (c) [y: f(y) = −1].
उत्तर
f (x) = x2
Range of f = R+ (Set of all real numbers greater than or equal to zero)
(b) Given:
f (x) = x2
⇒ x2 = 4
⇒ x = ± 2
∴ {x : f (x) = 4 } = { -2,2} .
(c) { y : f (y) = - 1}
⇒ f (y) = - 1
It is clear that x2 = -1 but x2 ≥ 0 .
⇒ f (y) ≠ -1
∴ {y : f (y) = -1} = Φ
APPEARS IN
संबंधित प्रश्न
What is the fundamental difference between a relation and a function? Is every relation a function?
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
(a) f1 = {(1, 1), (2, 11), (3, 1), (4, 15)}
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iv) \[\frac{f}{g}\]
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(iii) \[\frac{f}{g}\]
Let f(x) = x2 and g(x) = 2x+ 1 be two real functions. Find (f + g) (x), (f − g) (x), (fg) (x) and \[\left( \frac{f}{g} \right) \left( x \right)\] .
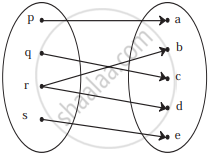
Check if the following relation is function:
If f(m) = m2 − 3m + 1, find f(−3)
If f(m) = m2 − 3m + 1, find `f(1/2)`
Which of the following relations are functions? If it is a function determine its domain and range:
{(0, 0), (1, 1), (1, −1), (4, 2), (4, −2), (9, 3), (9, −3), (16, 4), (16, −4)}
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b.
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(0)
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 2), (2, −1), (3, 1), (4, 3)}
If f(m) = m2 − 3m + 1, find f(x + 1)
If f(x) = `("a" - x)/("b" - x)`, f(2) is undefined, and f(3) = 5, find a and b
Express the following exponential equation in logarithmic form
3–4 = `1/81`
Express the following exponential equation in logarithmic form
e2 = 7.3890
Express the following exponential equation in logarithmic form
`"e"^(1/2)` = 1.6487
Find the domain of f(x) = log10 (x2 − 5x + 6)
Solve for x.
log2 x + log4 x + log16 x = `21/4`
A function f is defined as : f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 3
Answer the following:
Let f : R → R be given by f(x) = x + 5 for all x ∈ R. Draw its graph
Answer the following:
Solve : `sqrt(log_2 x^4) + 4log_4 sqrt(2/x)` = 2
Answer the following:
If `log"a"/(x + y - 2z) = log"b"/(y + z - 2x) = log"c"/(z + x - 2y)`, show that abc = 1
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - x^2) + sqrt(5 - x)`
A graph representing the function f(x) is given in it is clear that f(9) = 2
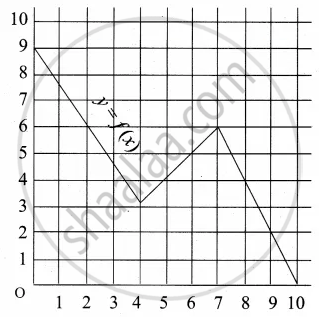
Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
Let f(x) = 2x + 5. If x ≠ 0 then find `(f(x + 2) -"f"(2))/x`
A plane is flying at a speed of 500 km per hour. Express the distance ‘d’ travelled by the plane as function of time t in hour
If a function f(x) is given as f(x) = x2 – 6x + 4 for all x ∈ R, then f(–3) = ______.
The domain of the function f(x) = log3+x (x2 - 1) is ______.
Find the domain for which the functions f(x) = 2x2 – 1 and g(x) = 1 – 3x are equal.
Find the range of the following functions given by `sqrt(16 - x^2)`
If f(x) = `x^3 - 1/x^3`, then `f(x) + f(1/x)` is equal to ______.
Let f and g be two functions given by f = {(2, 4), (5, 6), (8, – 1), (10, – 3)} g = {(2, 5), (7, 1), (8, 4), (10, 13), (11, – 5)} then. Domain of f + g is ______.
Let f(x) = `sqrt(1 + x^2)`, then ______.
The domain for which the functions defined by f(x) = 3x2 – 1 and g(x) = 3 + x are equal is ______.
Let f(x) and g(x) be two real polynomials of degree 2 and 1 respectively. If f(g(x)) = 8x2 – 2x, and g(f(x)) = 4x2 + 6x + 1, then the value of f(2) + g(2) is ______.
If f(x) = `log_e{((1 - x))/((1 - x))}, |x| < 1, f{(2x)/((1 + x^2))}` is equal to ______.
If f: R `rightarrow` R be a function defined by f(x) = 4x3 – 7. Then ______.
