Advertisements
Advertisements
प्रश्न
If f(x) = y = `(ax - b)/(cx - a)`, then prove that f(y) = x.
उत्तर
We have, f(x) = y = `(ax - b)/(cx - a)`
∴ f(y) = `(ay - b)/(cy - a)`
= `(a((ax - b)/(cx - a)) - b)/(c((ax - b)/(cx - a)) - a)`
= `(a(ax - b) - b(cx - a))/(c(ax - b) - a(cx - a))`
= `(a^2x - ab - bcx + ab)/(acx - bc - acx + a^2)`
= `(a^2x - bcx)/(a^2 - bc)`
= `(x(a^2 - bc))/((a^2 - bc))`
∴ f(y) = x
APPEARS IN
संबंधित प्रश्न
Let A = {9, 10, 11, 12, 13} and let f: A → N be defined by f(n) = the highest prime factor of n. Find the range of f.
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
(b) f2 = {(1, 1), (2, 7), (3, 5)}
Write the domain and range of function f(x) given by \[f\left( x \right) = \sqrt{\left[ x \right] - x}\] .
The range of the function \[f\left( x \right) = \frac{x^2 - x}{x^2 + 2x}\] is
The function f : R → R is defined by f(x) = cos2 x + sin4 x. Then, f(R) =
If f(x) = sin [π2] x + sin [−π]2 x, where [x] denotes the greatest integer less than or equal to x, then
The domain of definition of \[f\left( x \right) = \sqrt{x - 3 - 2\sqrt{x - 4}} - \sqrt{x - 3 + 2\sqrt{x - 4}}\] is
Check the injectivity and surjectivity of the following function.
f : Z → Z given by f(x) = x2
Express the following exponential equation in logarithmic form
54° = 1
Express the following logarithmic equation in exponential form
In `1/2` = – 0.693
Solve for x.
2 log10 x = `1 + log_10 (x + 11/10)`
Select the correct answer from given alternatives.
If f(x) =`1/(1 - x)`, then f{f[f(x)]} is
Answer the following:
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b
Answer the following:
Solve for x, logx (8x – 3) – logx 4 = 2
Answer the following:
If a2 + b2 = 7ab, show that, `log(("a" + "b")/3) = 1/2 log "a" + 1/2 log "b"`
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - x^2) + sqrt(5 - x)`
A graph representing the function f(x) is given in it is clear that f(9) = 2
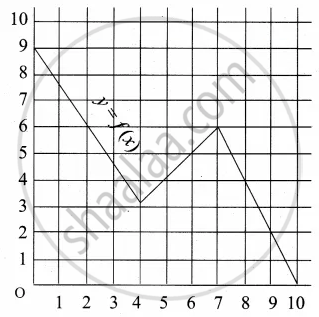
Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
A graph representing the function f(x) is given in it is clear that f(9) = 2
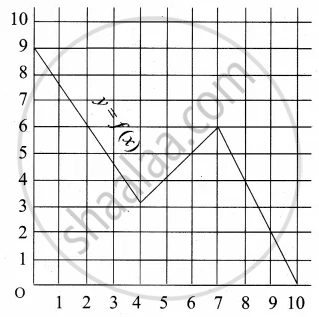
Describe the following Range
A plane is flying at a speed of 500 km per hour. Express the distance ‘d’ travelled by the plane as function of time t in hour
If f(x) = 5x - 3, then f-1(x) is ______
The domain of the real valued function f(x) = `sqrt((x - 2)/(3 - x))` is ______.
If f(x) = `{{:(x^2",", x ≥ 0),(x^3",", x < 0):}`, then f(x) is ______.
Find the domain for which the functions f(x) = 2x2 – 1 and g(x) = 1 – 3x are equal.
Find the domain of the following functions given by f(x) = `1/sqrt(x + |x|)`
Find the range of the following functions given by f(x) = `3/(2 - x^2)`
Find the range of the following functions given by f(x) = 1 – |x – 2|
If f(x) = `log_e{((1 - x))/((1 - x))}, |x| < 1, f{(2x)/((1 + x^2))}` is equal to ______.
The ratio `(2^(log_2 1/4 a) - 3^(log_27(a^2 + 1)^3) - 2a)/(7^(4log_49a) - a - 1)` simplifies to ______.
If f : R – {2} `rightarrow` R i s a function defined by f(x) = `(x^2 - 4)/(x - 2)`, then its range is ______.
lf f : [0, ∞) `rightarrow` [0, ∞) and f(x) = `x/(1 + x)`, then f is ______.
