Advertisements
Advertisements
प्रश्न
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
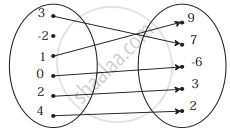
(b) f2 = {(1, 1), (2, 7), (3, 5)}
उत्तर
(b) Given:
f2 = {(1, 1), (2, 7), (3, 5)}
f2 is not a function from X to Y because 2 ∈ X has no image in Y.
APPEARS IN
संबंधित प्रश्न
find: f(1), f(−1), f(0) and f(2).
A function f : R → R is defined by f(x) = x2. Determine (a) range of f, (b) {x : f(x) = 4}, (c) [y: f(y) = −1].
If f(x) = (a − xn)1/n, a > 0 and n ∈ N, then prove that f(f(x)) = x for all x.
Write the range of the function f(x) = ex−[x], x ∈ R.
If \[f\left( x \right) = \log \left( \frac{1 + x}{1 - x} \right) \text{ and} g\left( x \right) = \frac{3x + x^3}{1 + 3 x^2}\] , then f(g(x)) is equal to
If f(x) = cos (log x), then value of \[f\left( x \right) f\left( 4 \right) - \frac{1}{2} \left\{ f\left( \frac{x}{4} \right) + f\left( 4x \right) \right\}\] is
If f : R → R and g : R → R are defined by f(x) = 2x + 3 and g(x) = x2 + 7, then the values of x such that g(f(x)) = 8 are
If f : [−2, 2] → R is defined by \[f\left( x \right) = \begin{cases}- 1, & \text{ for } - 2 \leq x \leq 0 \\ x - 1, & \text{ for } 0 \leq x \leq 2\end{cases}\] , then
{x ∈ [−2, 2] : x ≤ 0 and f (|x|) = x} =
If f : R → R be given by for all \[f\left( x \right) = \frac{4^x}{4^x + 2}\] x ∈ R, then
If \[\left[ x \right]^2 - 5\left[ x \right] + 6 = 0\], where [.] denotes the greatest integer function, then
Check if the following relation is function:
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(3)
If f(x) = 3x + a and f(1) = 7 find a and f(4).
Which sets of ordered pairs represent functions from A = {1, 2, 3, 4} to B = {−1, 0, 1, 2, 3}? Justify.
{(1, 0), (3, 3), (2, −1), (4, 1), (2, 2)}
Check if the relation given by the equation represents y as function of x:
x + y2 = 9
If f(m) = m2 − 3m + 1, find f(x + 1)
Express the area A of a square as a function of its side s
Express the following exponential equation in logarithmic form
e2 = 7.3890
Write the following expression as sum or difference of logarithm
`log ("pq"/"rs")`
Write the following expression as a single logarithm.
5 log x + 7 log y − log z
If x = loga bc, y = logb ca, z = logc ab then prove that `1/(1 + x) + 1/(1 + y) + 1/(1 + z)` = 1
Select the correct answer from given alternatives.
If f : R → R is defined by f(x) = x3 then f–1 (8) is equal to :
Answer the following:
A function f is defined as f(x) = 4x + 5, for – 4 ≤ x < 0. Find the values of f(–1), f(–2), f(0), if they exist
Answer the following:
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b
Answer the following:
Show that `7log (15/16) + 6log(8/3) + 5log (2/5) + log(32/25)` = log 3
Answer the following:
Find the domain of the following function.
f(x) = `(x^2 + 4x + 4)/(x^2 + x - 6)`
Answer the following:
Find the range of the following function.
f(x) = [x] – x
A function f is defined by f(x) = 3 – 2x. Find x such that f(x2) = (f(x))2
The domain of the function f(x) = `sqrtx` is ______.
If f(x) = 5x - 3, then f-1(x) is ______
Find the domain of the following function.
f(x) = [x] + x
Find the range of the following functions given by `|x - 4|/(x - 4)`
Find the domain of the following functions given by f(x) = `(x^3 - x + 3)/(x^2 - 1)`
Find the range of the following functions given by f(x) = 1 + 3 cos2x
(Hint: –1 ≤ cos 2x ≤ 1 ⇒ –3 ≤ 3 cos 2x ≤ 3 ⇒ –2 ≤ 1 + 3cos 2x ≤ 4)
Let f(x) = `sqrt(1 + x^2)`, then ______.
The function f: R `rightarrow` R defined by f(x) = sin x is ______.
The period of the function
f(x) = `(sin 8x cos x - sin 6x cos 3x)/(cos 2x cos x - sin 3x sin 4x)` is ______.
