Advertisements
Advertisements
प्रश्न
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
(b) f2 = {(1, 1), (2, 7), (3, 5)}
उत्तर
(b) Given:
f2 = {(1, 1), (2, 7), (3, 5)}
f2 is not a function from X to Y because 2 ∈ X has no image in Y.
APPEARS IN
संबंधित प्रश्न
Let f : R+ → R, where R+ is the set of all positive real numbers, such that f(x) = loge x. Determine
(a) the image set of the domain of f
If f(x) = (x − a)2 (x − b)2, find f(a + b).
If \[f\left( x \right) = \frac{1}{1 - x}\] , show that f[f[f(x)]] = x.
If \[f\left( x \right) = \frac{2x}{1 + x^2}\] , show that f(tan θ) = sin 2θ.
If f(x) = cos [π2]x + cos [−π2] x, where [x] denotes the greatest integer less than or equal to x, then write the value of f(π).
Write the range of the function f(x) = ex−[x], x ∈ R.
Find the set of values of x for which the functions f(x) = 3x2 − 1 and g(x) = 3 + x are equal.
If f(x) = cos (log x), then the value of f(x) f(y) −\[\frac{1}{2}\left\{ f\left( \frac{x}{y} \right) + f\left( xy \right) \right\}\] is
Let f(x) = x, \[g\left( x \right) = \frac{1}{x}\] and h(x) = f(x) g(x). Then, h(x) = 1
If f(m) = m2 − 3m + 1, find `f(1/2)`
Which of the following relations are functions? If it is a function determine its domain and range:
{(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
A function f is defined as follows: f(x) = 4x + 5, for −4 ≤ x < 0. Find the values of f(−1), f(−2), f(0), if they exist.
A function f is defined as follows: f(x) = 5 − x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 3
Check if the following relation is a function.
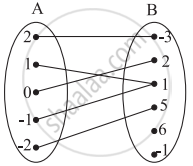
Check if the following relation is a function.
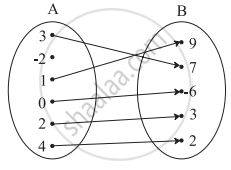
Check the injectivity and surjectivity of the following function.
f : R → R given by f(x) = x3
Express the following exponential equation in logarithmic form
25 = 32
Express the following exponential equation in logarithmic form
3–4 = `1/81`
Write the following expression as a single logarithm.
5 log x + 7 log y − log z
Given that log 2 = a and log 3 = b, write `log sqrt(96)` in terms of a and b
Prove that logbm a = `1/"m" log_"b""a"`
If f(x) = ax2 − bx + 6 and f(2) = 3 and f(4) = 30, find a and b
Solve for x.
log2 + log(x + 3) – log(3x – 5) = log3
If `log((x + y)/3) = 1/2 log x + 1/2 logy`, show that `x/y + y/x` = 7
The equation logx2 16 + log2x 64 = 3 has,
Select the correct answer from given alternative.
The domain and range of f(x) = 2 − |x − 5| is
A function f is defined as : f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 3
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Answer the following:
If `log ((x - y)/5) = 1/2 logx + 1/2 log y`, show that x2 + y2 = 27xy
Answer the following:
Show that `7log (15/16) + 6log(8/3) + 5log (2/5) + log(32/25)` = log 3
Answer the following:
Find the range of the following function.
f(x) = |x – 5|
Given the function f: x → x2 – 5x + 6, evaluate f(2a)
Given the function f: x → x2 – 5x + 6, evaluate f(2)
The data in the adjacent table depicts the length of a person's forehand and their corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length (x) as y = ax + b, where a, b are constant.
| Length ‘x’ of forehand (in cm) |
Height 'y' (in inches) |
| 35 | 56 |
| 45 | 65 |
| 50 | 69.5 |
| 55 | 74 |
Find the length of forehand of a person if the height is 53.3 inches
Mapping f: R → R which is defined as f(x) = sin x, x ∈ R will be ______
Find the range of the following functions given by f(x) = 1 + 3 cos2x
(Hint: –1 ≤ cos 2x ≤ 1 ⇒ –3 ≤ 3 cos 2x ≤ 3 ⇒ –2 ≤ 1 + 3cos 2x ≤ 4)
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f + g)(x)
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (fg)(x)
The ratio `(2^(log_2 1/4 a) - 3^(log_27(a^2 + 1)^3) - 2a)/(7^(4log_49a) - a - 1)` simplifies to ______.
If f: R `rightarrow` R be a function defined by f(x) = 4x3 – 7. Then ______.
