Advertisements
Advertisements
प्रश्न
Find the range of the following functions given by f(x) = |x − 3|
उत्तर
We know |x| are defined for all real values.
And |x – 3| will always be greater than or equal to 0.
i.e., f(x) ≥ 0
Therefore, the range of f = `[0, oo)`
APPEARS IN
संबंधित प्रश्न
Let f : [0, ∞) → R and g : R → R be defined by \[f\left( x \right) = \sqrt{x}\] and g(x) = x. Find f + g, f − g, fg and \[\frac{f}{g}\] .
Write the range of the function f(x) = ex−[x], x ∈ R.
The domain of the function \[f\left( x \right) = \sqrt{5 \left| x \right| - x^2 - 6}\] is
The range of the function f(x) = |x − 1| is
If f(m) = m2 − 3m + 1, find f(− x)
Which of the following relations are functions? If it is a function determine its domain and range:
{(1, 1), (3, 1), (5, 2)}
Check if the following relation is a function.
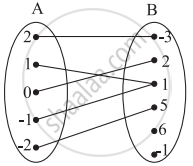
Check if the following relation is a function.
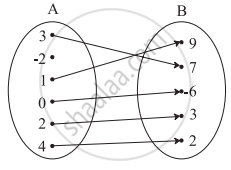
If f(m) = m2 − 3m + 1, find f(x + 1)
If f(m) = m2 − 3m + 1, find f(− x)
Find x, if g(x) = 0 where g(x) = `(18 -2x^2)/7`
Express the area A of a square as a function of its side s
Express the area A of circle as a function of its circumference C.
Express the following exponential equation in logarithmic form
3–4 = `1/81`
Express the following exponential equation in logarithmic form
10−2 = 0.01
Write the following expression as a single logarithm.
ln (x + 2) + ln (x − 2) − 3 ln (x + 5)
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f − g) (2)
Select the correct answer from given alternatives
If f(x) = 2x2 + bx + c and f(0) = 3 and f(2) = 1, then f(1) is equal to
Answer the following:
Let f: R → R be a function defined by f(x) = 5x3 – 8 for all x ∈ R, show that f is one-one and onto. Hence find f –1
Answer the following:
Let f : R → R be given by f(x) = x + 5 for all x ∈ R. Draw its graph
Answer the following:
Simplify `log_10 28/45 - log_10 35/324 + log_10 325/432 - log_10 13/15`
Given the function f: x → x2 – 5x + 6, evaluate f(x – 1)
The domain of the function f(x) = `sqrtx` is ______.
Mapping f: R → R which is defined as f(x) = sin x, x ∈ R will be ______
Find the range of the following functions given by f(x) = 1 – |x – 2|
Redefine the function f(x) = x − 2 + 2 + x , – 3 ≤ x ≤ 3
The domain of the function f defined by f(x) = `sqrt(4 - x) + 1/sqrt(x^2 - 1)` is equal to ______.
The domain and range of real function f defined by f(x) = `sqrt(x - 1)` is given by ______.
Which of the following functions is NOT one-one?
The range of the function f(x) = x2 + 2x+ 2 is ______.
