Advertisements
Advertisements
प्रश्न
Range of f(x) = `1/(1 - 2 cosx)` is ______.
विकल्प
`[1/3, 1]`
`[-1, 1/3]`
`(-oo, -1] ∪ [1/3, oo)`
`[- 1/3, 1]`
उत्तर
Range of f(x) = `1/(1 - 2 cosx)` is `[-1, 1/3]`.
Explanation:
Given that: `1/(1 - 2 cosx)`
We know that – 1 ≤ cos x ≤ 1
⇒ 1 ≥ cos x ≥ – 1
⇒ – 1 ≤ – cos x ≤ 1
⇒ – 2 ≤ – 2 cos x ≤ 2
⇒ – 2 + 1 ≤ 1 – 2 cos x ≤ 2 + 1
⇒ – 1 ≤ 1 – 2 cos x ≤ 3
⇒ – 1 ≤ `1/(1 - 2 cosx) ≤ 1/3`
⇒ `– 1 ≤ "f"(x) ≤ 1/3`
So the range of f(x) = `[-1, 1/3]`
APPEARS IN
संबंधित प्रश्न
Let A = {−2, −1, 0, 1, 2} and f : A → Z be a function defined by f(x) = x2 − 2x − 3. Find:
(b) pre-images of 6, −3 and 5.
A function f : R → R is defined by f(x) = x2. Determine (a) range of f, (b) {x : f(x) = 4}, (c) [y: f(y) = −1].
Let f : R → R and g : C → C be two functions defined as f(x) = x2 and g(x) = x2. Are they equal functions?
f, g, h are three function defined from R to R as follow:
(i) f(x) = x2
Find the range of function.
If f(x) = (x − a)2 (x − b)2, find f(a + b).
If \[f\left( x \right) = \begin{cases}x^2 , & \text{ when } x < 0 \\ x, & \text{ when } 0 \leq x < 1 \\ \frac{1}{x}, & \text{ when } x \geq 1\end{cases}\]
find: (a) f(1/2), (b) f(−2), (c) f(1), (d)
Write the domain and range of function f(x) given by
Let f and g be two real functions given by
f = {(0, 1), (2, 0), (3, −4), (4, 2), (5, 1)} and g = {(1, 0), (2, 2), (3, −1), (4, 4), (5, 3)}
Find the domain of fg.
The domain of the function
The domain of the function \[f\left( x \right) = \sqrt{5 \left| x \right| - x^2 - 6}\] is
A function f is defined as follows: f(x) = 4x + 5, for −4 ≤ x < 0. Find the values of f(−1), f(−2), f(0), if they exist.
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(0)
Check if the following relation is a function.
Check if the relation given by the equation represents y as function of x:
3x − 6 = 21
Check the injectivity and surjectivity of the following function.
f : Z → Z given by f(x) = x2
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x3
Express the following exponential equation in logarithmic form
`"e"^(1/2)` = 1.6487
Select the correct answer from given alternatives.
Find x, if 2log2 x = 4
Select the correct answer from given alternatives
If f(x) = 2x2 + bx + c and f(0) = 3 and f(2) = 1, then f(1) is equal to
A function f is defined as : f(x) = 5 – x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 3
Answer the following:
If `log (("a" + "b")/2) = 1/2(log"a" + log"b")`, then show that a = b
Answer the following:
Without using log tables, prove that `2/5 < log_10 3 < 1/2`
Let X = {3, 4, 6, 8}. Determine whether the relation R = {(x, f(x)) | x ∈ X, f(x) = x2 + 1} is a function from X to N?
A graph representing the function f(x) is given in it is clear that f(9) = 2
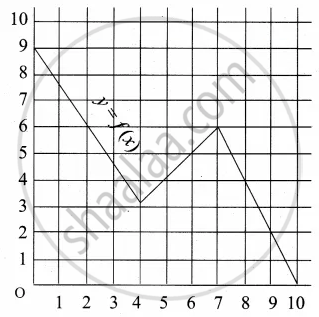
Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
Mapping f: R → R which is defined as f(x) = sin x, x ∈ R will be ______
Find the domain of the following function.
f(x) = [x] + x
Find the range of the following functions given by `|x - 4|/(x - 4)`
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f – g)(x)
The domain and range of the real function f defined by f(x) = `(4 - x)/(x - 4)` is given by ______.
The domain of the function f(x) = `1/sqrt(|x| - x)` is ______.
