Advertisements
Advertisements
Question
If f(x) = (a − xn)1/n, a > 0 and n ∈ N, then prove that f(f(x)) = x for all x.
Solution
Given:
f(x) = (a − xn)1/n, a > 0
Now,
f{ f (x)} = f (a − xn)1/n
= [a – {(a – xn)1/n}n]1/n
= [ a – (a – xn)]1/n
= [ a – a + xn)]1/n = (xn)1/n = x(n × 1/n) = x
Thus, f(f(x)) = x.
Hence proved.
APPEARS IN
RELATED QUESTIONS
Let A = {9, 10, 11, 12, 13} and let f: A → N be defined by f(n) = the highest prime factor of n. Find the range of f.
What is the fundamental difference between a relation and a function? Is every relation a function?
Let f : R+ → R, where R+ is the set of all positive real numbers, such that f(x) = loge x. Determine
(b) {x : f(x) = −2}
f, g, h are three function defined from R to R as follow:
(ii) g(x) = sin x
Find the range of function.
If f(x) = (x − a)2 (x − b)2, find f(a + b).
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(i) f + g
If f(x) = cos (loge x), then \[f\left( \frac{1}{x} \right)f\left( \frac{1}{y} \right) - \frac{1}{2}\left\{ f\left( xy \right) + f\left( \frac{x}{y} \right) \right\}\] is equal to
The function f : R → R is defined by f(x) = cos2 x + sin4 x. Then, f(R) =
The domain of definition of \[f\left( x \right) = \sqrt{\frac{x + 3}{\left( 2 - x \right) \left( x - 5 \right)}}\] is
The domain of the function \[f\left( x \right) = \sqrt{\frac{\left( x + 1 \right) \left( x - 3 \right)}{x - 2}}\] is
The domain of definition of \[f\left( x \right) = \sqrt{x - 3 - 2\sqrt{x - 4}} - \sqrt{x - 3 + 2\sqrt{x - 4}}\] is
The range of the function f(x) = |x − 1| is
Check if the following relation is a function.
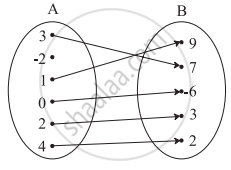
Find x, if g(x) = 0 where g(x) = 6x2 + x − 2
Express the area A of circle as a function of its radius r
An open box is made from a square of cardboard of 30 cms side, by cutting squares of length x centimeters from each corner and folding the sides up. Express the volume of the box as a function of x. Also find its domain
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x3
Prove that `"b"^(log_"b""a"` = a
If `log((x + y)/3) = 1/2 log x + 1/2 logy`, show that `x/y + y/x` = 7
Select the correct answer from given alternatives.
If f(x) =`1/(1 - x)`, then f{f[f(x)]} is
Select the correct answer from given alternatives
The domain of `1/([x] - x)` where [x] is greatest integer function is
Answer the following:
Identify the following relation is the function? If it is a function determine its domain and range.
{(0, 0), (1, 1), (1, –1), (4, 2), (4, –2), (9, 3), (9, –3), (16, 4), (16, –4)}
Answer the following:
If f(x) = 3x4 – 5x2 + 7 find f(x – 1)
Answer the following:
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b
Answer the following:
If `log_2"a"/4 = log_2"b"/6 = log_2"c"/(3"k")` and a3b2c = 1 find the value of k
Answer the following:
Find the domain of the following function.
f(x) = `(x^2 + 4x + 4)/(x^2 + x - 6)`
Answer the following:
Find the domain of the following function.
f(x) = `sqrt(x - 3) + 1/(log(5 - x))`
Answer the following:
Find the range of the following function.
f(x) = 1 + 2x + 4x
Answer the following:
Find (f ° g) (x) and (g ° f) (x)
f(x) = `x/(x + 1)`, g(x) = `x/(1 - x)`
Let X = {3, 4, 6, 8}. Determine whether the relation R = {(x, f(x)) | x ∈ X, f(x) = x2 + 1} is a function from X to N?
A graph representing the function f(x) is given in it is clear that f(9) = 2
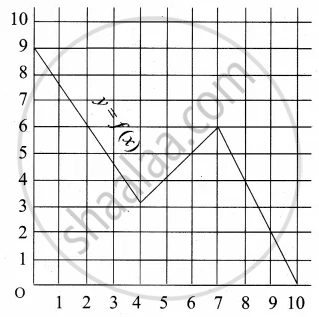
Describe the following Range
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Calculate the value of `"gg" (1/2)`
The range of 7, 11, 16, 27, 31, 33, 42, 49 is ______.
The domain of the function f(x) = `sqrtx` is ______.
If f(x) = `1/sqrt(4 - 3x)`, then dom(f) = ______..
Find the domain of the following function.
f(x) = [x] + x
Find the domain of the function f given by f(x) = `1/sqrt([x]^2 - [x] - 6)`
If f(x) = y = `(ax - b)/(cx - a)`, then prove that f(y) = x.
The domain and range of the real function f defined by f(x) = `(4 - x)/(x - 4)` is given by ______.
The domain for which the functions defined by f(x) = 3x2 – 1 and g(x) = 3 + x are equal is ______.
