Advertisements
Advertisements
Question
Select the correct answer from given alternatives.
If f(x) =`1/(1 - x)`, then f{f[f(x)]} is
Options
x – 1
1 – x
x
– x
Solution
x
Explanation;
f[f(x)] = `"f"(1/(1 - x))`
= `1/(1 - 1/(1 - x))`
= `1/(((1 - x) - 1)/(1 - x))`
= `(x - 1)/x`
∴ f{f[f(x)]} = `"f"((x - 1)/x)`
= `1/(1 - (x - 1)/x)`
= `1/((x - (x - 1))/x`
= x
APPEARS IN
RELATED QUESTIONS
Let A = {−2, −1, 0, 1, 2} and f : A → Z be a function defined by f(x) = x2 − 2x − 3. Find:
(a) range of f, i.e. f(A).
If f(x) = x2 − 3x + 4, then find the values of x satisfying the equation f(x) = f(2x + 1).
If f(x) = 4x − x2, x ∈ R, then write the value of f(a + 1) −f(a − 1).
Write the domain and range of function f(x) given by
Let A and B be two sets such that n(A) = p and n(B) = q, write the number of functions from A to B.
If f : Q → Q is defined as f(x) = x2, then f−1 (9) is equal to
Let f(x) = |x − 1|. Then,
If \[f\left( x \right) = \log \left( \frac{1 + x}{1 - x} \right)\] , then \[f\left( \frac{2x}{1 + x^2} \right)\] is equal to
The range of the function \[f\left( x \right) = \frac{x^2 - x}{x^2 + 2x}\] is
If f : R → R and g : R → R are defined by f(x) = 2x + 3 and g(x) = x2 + 7, then the values of x such that g(f(x)) = 8 are
If \[3f\left( x \right) + 5f\left( \frac{1}{x} \right) = \frac{1}{x} - 3\] for all non-zero x, then f(x) =
The domain of definition of \[f\left( x \right) = \sqrt{\frac{x + 3}{\left( 2 - x \right) \left( x - 5 \right)}}\] is
The domain of definition of \[f\left( x \right) = \sqrt{x - 3 - 2\sqrt{x - 4}} - \sqrt{x - 3 + 2\sqrt{x - 4}}\] is
The domain of the function \[f\left( x \right) = \sqrt{5 \left| x \right| - x^2 - 6}\] is
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(2)
Check if the following relation is a function.
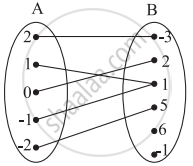
Find the domain and range of the follwoing function.
h(x) = `sqrt(x + 5)/(5 + x)`
Check the injectivity and surjectivity of the following function.
f : R → R given by f(x) = x3
Express the following exponential equation in logarithmic form
25 = 32
Express the following exponential equation in logarithmic form
3–4 = `1/81`
Express the following exponential equation in logarithmic form
10−2 = 0.01
Find the domain of f(x) = ln (x − 5)
Write the following expression as sum or difference of logarithm
`log (sqrt(x) root(3)(y))`
Write the following expression as a single logarithm.
5 log x + 7 log y − log z
Prove that `"b"^(log_"b""a"` = a
Solve for x.
x + log10 (1 + 2x) = x log10 5 + log10 6
Select the correct answer from given alternative.
The domain and range of f(x) = 2 − |x − 5| is
Answer the following:
Let f : R → R be given by f(x) = x3 + 1 for all x ∈ R. Draw its graph
Answer the following:
If f(x) = log(1 – x), 0 ≤ x < 1 show that `"f"(1/(1 + x))` = f(1 – x) – f(– x)
A plane is flying at a speed of 500 km per hour. Express the distance ‘d’ travelled by the plane as function of time t in hour
The range of the function f(x) = `(x^2 - 3x + 2)/(x^3 - 4x^2 + 5x - 2)` is ______
The domain and range of the real function f defined by f(x) = `(4 - x)/(x - 4)` is given by ______.
The domain and range of the function f given by f(x) = 2 – |x – 5| is ______.
The value of the function f(x) = `(x^2 - 3x + 2)/(x^2 + x - 6)` lies in the interval
Let f(x) and g(x) be two real polynomials of degree 2 and 1 respectively. If f(g(x)) = 8x2 – 2x, and g(f(x)) = 4x2 + 6x + 1, then the value of f(2) + g(2) is ______.
The range of the function y = `1/(2 - sin3x)` is ______.
Let f be a function with domain [–3, 5] and let g(x) = | 3x + 4 |. Then, the domain of (fog) (x) is ______.
