Advertisements
Advertisements
प्रश्न
Find the domain of the following functions given by f(x) = x|x|
उत्तर
We know x and |x| are defined for all real values.
Therefore, the domain of f = R
APPEARS IN
संबंधित प्रश्न
What is the fundamental difference between a relation and a function? Is every relation a function?
Let f : R+ → R, where R+ is the set of all positive real numbers, such that f(x) = loge x. Determine
(c) whether f(xy) = f(x) : f(y) holds
If \[f\left( x \right) = \frac{x - 1}{x + 1}\] , then show that
(i) \[f\left( \frac{1}{x} \right) = - f\left( x \right)\]
(ii) \[f\left( - \frac{1}{x} \right) = - \frac{1}{f\left( x \right)}\]
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(ii) g − f
If f, g and h are real functions defined by
Let f(x) = x2 and g(x) = 2x+ 1 be two real functions. Find (f + g) (x), (f − g) (x), (fg) (x) and \[\left( \frac{f}{g} \right) \left( x \right)\] .
Let \[f\left( x \right) = \frac{\alpha x}{x + 1}, x \neq - 1\] . Then write the value of α satisfying f(f(x)) = x for all x ≠ −1.
If f, g, h are real functions given by f(x) = x2, g(x) = tan x and h(x) = loge x, then write the value of (hogof)\[\left( \sqrt{\frac{\pi}{4}} \right)\] .
If \[f\left( x \right) = \frac{2^x + 2^{- x}}{2}\] , then f(x + y) f(x − y) is equal to
If \[f\left( x \right) = \frac{\sin^4 x + \cos^2 x}{\sin^2 x + \cos^4 x}\] for x ∈ R, then f (2002) =
The domain of definition of \[f\left( x \right) = \sqrt{x - 3 - 2\sqrt{x - 4}} - \sqrt{x - 3 + 2\sqrt{x - 4}}\] is
Check if the following relation is function:
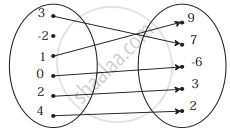
If f(m) = m2 − 3m + 1, find f(0)
Check if the relation given by the equation represents y as function of x:
2y + 10 = 0
If f(m) = m2 − 3m + 1, find f(−3)
Find x, if g(x) = 0 where g(x) = 6x2 + x − 2
Find x, if f(x) = g(x) where f(x) = x4 + 2x2, g(x) = 11x2
Find the domain and range of the following function.
f(x) = 7x2 + 4x − 1
Express the following exponential equation in logarithmic form
231 = 23
Given that log 2 = a and log 3 = b, write `log sqrt(96)` in terms of a and b
Prove that alogcb = blogca
Solve for x.
log2 x + log4 x + log16 x = `21/4`
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f − g) (2)
Answer the following:
If `log"a"/(x + y - 2z) = log"b"/(y + z - 2x) = log"c"/(z + x - 2y)`, show that abc = 1
Find the domain of the following function.
f(x) = `sqrtlog(x^2 - 6x + 6)`
Answer the following:
Find the range of the following function.
f(x) = `x/(9 + x^2)`
The domain of the function f(x) = log3+x (x2 - 1) is ______.
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (fg)(x)
The domain of the function f(x) = `sin^-1((|x| + 5)/(x^2 + 1))` is (–∞, –a] ≈ [a, ∞). Then a is equal to ______.
If f: R `rightarrow` R be a function defined by f(x) = 4x3 – 7. Then ______.
