Advertisements
Advertisements
प्रश्न
Find the domain and range of the following function.
f(x) = 7x2 + 4x − 1
उत्तर १
f(x) = 7x2 + 4x − 1
f is defined for all x
∴ Domain of f = R (i.e. the set of real numbers)
7x2 + 4x − 1
= `7(x^2 + 4/7x) - 1`
= `7(x + 2/7)^2 - 1 - 4/7`
= `7(x + 2/7)^2 - 11/7 ≥ - 11/7`
∴ Range of f = `[-11/7, ∞)`
उत्तर २
f(x) = 7x2 + 4x - 1
f(x) is defined for all x ∈ R
∴ Domain = R
7x2 + 4x − 1
`= 7[x^2 + 4/7x] - 1`
`= 7[x^2 + (4x)/7 + 4/49] - 28/49 - 1`
`= 7(x + 2/7)^2 - 77/49`
`= 7(x + 2/7)^2 - 11/7`
∴ `7(x + 2/7)^2 ≥ 0 "for all x ∈ R"`
∴ `7(x + 2/7)^2 - 11/7 ≥ 0 - 11/7 "for all x ∈ R"`
∴ `f(x) ≥ - 11/7 "for all x ∈ R"`
∴ Range = `[-11/7, ∞)`
∴ Domain = R, Range = `[-11/7, ∞).`
APPEARS IN
संबंधित प्रश्न
Let f be the subset of Z × Z defined by f = {(ab, a + b): a, b ∈ Z}. Is f a function from Z to Z: justify your answer.
If f(x) = x2 − 3x + 4, then find the values of x satisfying the equation f(x) = f(2x + 1).
If \[f\left( x \right) = \frac{1}{1 - x}\] , show that f[f[f(x)]] = x.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(v) \[\frac{g}{f}\]
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(i) f + g
If f(x) = cos [π2]x + cos [−π2] x, where [x] denotes the greatest integer less than or equal to x, then write the value of f(π).
If f(x) = 4x − x2, x ∈ R, then write the value of f(a + 1) −f(a − 1).
If \[f\left( x \right) = \log \left( \frac{1 + x}{1 - x} \right) \text{ and} g\left( x \right) = \frac{3x + x^3}{1 + 3 x^2}\] , then f(g(x)) is equal to
If \[f\left( x \right) = \frac{2^x + 2^{- x}}{2}\] , then f(x + y) f(x − y) is equal to
The domain of definition of \[f\left( x \right) = \sqrt{4x - x^2}\] is
The range of \[f\left( x \right) = \frac{1}{1 - 2\cos x}\] is
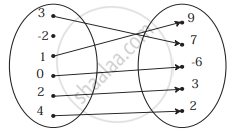
Check if the following relation is function:
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(3)
If f(m) = m2 − 3m + 1, find `f(1/2)`
Find the domain and range of the following function.
g(x) = `(x + 4)/(x - 2)`
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x2
Express the following exponential equation in logarithmic form
25 = 32
Solve for x.
x + log10 (1 + 2x) = x log10 5 + log10 6
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f + g) (x)
Select the correct answer from given alternatives.
Let the function f be defined by f(x) = `(2x + 1)/(1 - 3x)` then f–1 (x) is ______.
Select the correct answer from given alternative.
The domain and range of f(x) = 2 − |x − 5| is
Answer the following:
Find whether the following function is one-one
f : R → R defined by f(x) = x2 + 5
Answer the following:
Let f: R → R be a function defined by f(x) = 5x3 – 8 for all x ∈ R, show that f is one-one and onto. Hence find f –1
Answer the following:
If f(x) = ax2 + bx + 2 and f(1) = 3, f(4) = 42, find a and b
Answer the following:
Find the range of the following function.
f(x) = `1/(1 + sqrt(x))`
Let X = {3, 4, 6, 8}. Determine whether the relation R = {(x, f(x)) | x ∈ X, f(x) = x2 + 1} is a function from X to N?
A graph representing the function f(x) is given in it is clear that f(9) = 2
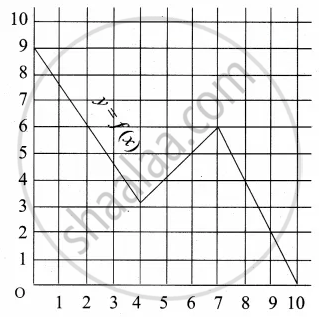
Describe the following Domain
A graph representing the function f(x) is given in it is clear that f(9) = 2
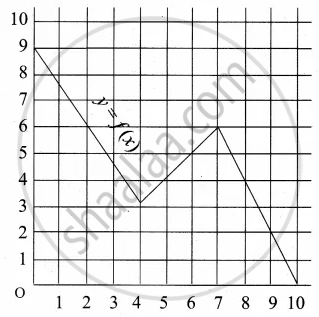
What is the image of 6 under f?
If the domain of function f(a) = a2 - 4a + 8 is (-∞, ∞), then the range of function is ______
The range of the function f(x) = `(x^2 - 3x + 2)/(x^3 - 4x^2 + 5x - 2)` is ______
If a function f(x) is given as f(x) = x2 – 6x + 4 for all x ∈ R, then f(–3) = ______.
Find the domain of the following function.
f(x) = `x/(x^2 + 3x + 2)`
Find the domain of the following functions given by f(x) = `(x^3 - x + 3)/(x^2 - 1)`
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find `(f/g)(x)`
The value of the function f(x) = `(x^2 - 3x + 2)/(x^2 + x - 6)` lies in the interval
The ratio `(2^(log_2 1/4 a) - 3^(log_27(a^2 + 1)^3) - 2a)/(7^(4log_49a) - a - 1)` simplifies to ______.
Which of the following functions is NOT one-one?
