Advertisements
Advertisements
प्रश्न
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (f – g)(x)
उत्तर
(f – g)(x)
⇒ (f – g)(x) = f(x) – g(x)
⇒ f(x) – g(x) = `sqrt(x) - x`
APPEARS IN
संबंधित प्रश्न
et A = (12, 13, 14, 15, 16, 17) and f : A → Z be a function given by
f(x) = highest prime factor of x.
Find range of f.
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(v) \[\frac{g}{f}\]
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(vi) \[2f - \sqrt{5} g\]
If A = {1, 2, 3} and B = {x, y}, then the number of functions that can be defined from A into B is
The function f : R → R is defined by f(x) = cos2 x + sin4 x. Then, f(R) =
If \[f\left( x \right) = 64 x^3 + \frac{1}{x^3}\] and α, β are the roots of \[4x + \frac{1}{x} = 3\] . Then,
The domain of definition of \[f\left( x \right) = \sqrt{x - 3 - 2\sqrt{x - 4}} - \sqrt{x - 3 + 2\sqrt{x - 4}}\] is
The range of \[f\left( x \right) = \frac{1}{1 - 2\cos x}\] is
If f(m) = m2 − 3m + 1, find `f(1/2)`
If f(x) = 3x + a and f(1) = 7 find a and f(4).
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(0)
Check if the relation given by the equation represents y as function of x:
2y + 10 = 0
Find x, if f(x) = g(x) where f(x) = `sqrt(x) - 3`, g(x) = 5 – x
Express the area A of a square as a function of its perimeter P
Express the area A of circle as a function of its circumference C.
Write the following expression as a single logarithm.
`1/3 log (x - 1) + 1/2 log (x)`
If f(x) = ax2 − bx + 6 and f(2) = 3 and f(4) = 30, find a and b
Solve for x.
log2 x + log4 x + log16 x = `21/4`
Select the correct answer from given alternatives.
If log (5x – 9) – log (x + 3) = log 2 then x = ...............
Answer the following:
For any base show that log (1 + 2 + 3) = log 1 + log 2 + log 3
Answer the following:
Without using log tables, prove that `2/5 < log_10 3 < 1/2`
Let f = {(x, y) | x, y ∈ N and y = 2x} be a relation on N. Find the domain, co-domain and range. Is this relation a function?
A graph representing the function f(x) is given in it is clear that f(9) = 2
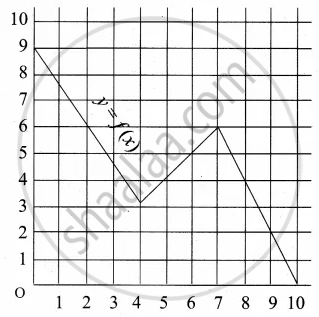
What is the image of 6 under f?
The range of the function f(x) = `(x - 3)/(5 - x)`, x ≠ 5 is ______.
Find the range of the following functions given by f(x) = `3/(2 - x^2)`
If f(x) = `(x - 1)/(x + 1)`, then show that `f(- 1/x) = (-1)/(f(x))`
The domain of the function f(x) = `sin^-1((|x| + 5)/(x^2 + 1))` is (–∞, –a] ≈ [a, ∞). Then a is equal to ______.
If f(x) = `log_e{((1 - x))/((1 - x))}, |x| < 1, f{(2x)/((1 + x^2))}` is equal to ______.
The function f: R `rightarrow` R defined by f(x) = sin x is ______.
