Advertisements
Advertisements
प्रश्न
If f : R → R and g : R → R are defined by f(x) = 2x + 3 and g(x) = x2 + 7, then the values of x such that g(f(x)) = 8 are
पर्याय
(a) 1, 2
(b) −1, 2
(c) −1, −2
(d) 1, −2
उत्तर
(c) −1, −2
f(x) = 2x + 3 and g(x) = x2 + 7
\[g(f(x)) = 8\]
\[ \Rightarrow \left( f(x) \right)^2 + 7 = 8\]
\[ \Rightarrow (2x + 3 )^2 + 7 = 8\]
\[ \Rightarrow x^2 + 3x + 2 = 0\]
\[ \Rightarrow (x + 2)(x + 1) = 0\]
\[ \Rightarrow x = - 1, - 2\]
APPEARS IN
संबंधित प्रश्न
f, g, h are three function defined from R to R as follow:
(ii) g(x) = sin x
Find the range of function.
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
(c) f3 = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
If \[f\left( x \right) = \frac{x - 1}{x + 1}\] , then show that
(i) \[f\left( \frac{1}{x} \right) = - f\left( x \right)\]
(ii) \[f\left( - \frac{1}{x} \right) = - \frac{1}{f\left( x \right)}\]
If for non-zero x, af(x) + bf \[\left( \frac{1}{x} \right) = \frac{1}{x} - 5\] , where a ≠ b, then find f(x).
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(v) \[\frac{g}{f}\]
If f(x) = loge (1 − x) and g(x) = [x], then determine function:
(ii) fg
Let A and B be two sets such that n(A) = p and n(B) = q, write the number of functions from A to B.
If f : [−2, 2] → R is defined by \[f\left( x \right) = \begin{cases}- 1, & \text{ for } - 2 \leq x \leq 0 \\ x - 1, & \text{ for } 0 \leq x \leq 2\end{cases}\] , then
{x ∈ [−2, 2] : x ≤ 0 and f (|x|) = x} =
If \[e^{f\left( x \right)} = \frac{10 + x}{10 - x}\] , x ∈ (−10, 10) and \[f\left( x \right) = kf\left( \frac{200 x}{100 + x^2} \right)\] , then k =
If \[f\left( x \right) = 64 x^3 + \frac{1}{x^3}\] and α, β are the roots of \[4x + \frac{1}{x} = 3\] . Then,
The domain of the function
The range of the function \[f\left( x \right) = \frac{x}{\left| x \right|}\] is
The range of the function \[f\left( x \right) = \frac{x + 2}{\left| x + 2 \right|}\],x ≠ −2 is
If f(x) = `{(x^2 + 3"," x ≤ 2),(5x + 7"," x > 2):},` then find f(3)
A function f is defined as follows: f(x) = 4x + 5, for −4 ≤ x < 0. Find the values of f(−1), f(−2), f(0), if they exist.
If f(m) = m2 − 3m + 1, find f(− x)
Find the domain and range of the following function.
f(x) = `sqrt((x - 3)/(7 - x))`
Find the domain and range of the following function.
f(x) = `sqrt(16 - x^2)`
Check the injectivity and surjectivity of the following function.
f : N → N given by f(x) = x2
Show that if f : A → B and g : B → C are one-one, then g ° f is also one-one
lf f(x) = 3(4x+1), find f(– 3)
Write the following expression as a single logarithm.
ln (x + 2) + ln (x − 2) − 3 ln (x + 5)
Answer the following:
If `log ((x - y)/5) = 1/2 logx + 1/2 log y`, show that x2 + y2 = 27xy
Answer the following:
If a2 = b3 = c4 = d5, show that loga bcd = `47/30`
A graph representing the function f(x) is given in it is clear that f(9) = 2
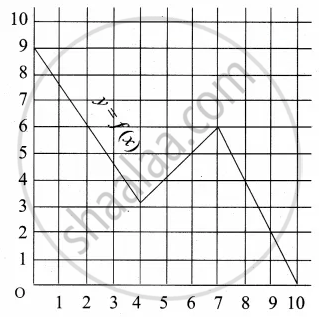
Describe the following Domain
The data in the adjacent table depicts the length of a person's forehand and their corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length (x) as y = ax + b, where a, b are constant.
| Length ‘x’ of forehand (in cm) |
Height 'y' (in inches) |
| 35 | 56 |
| 45 | 65 |
| 50 | 69.5 |
| 55 | 74 |
Find the height of a person whose forehand length is 40 cm
If f(x) = `(x - 1)/(x + 1), x ≠ - 1` Show that f(f(x)) = `- 1/x`, Provided x ≠ 0
The function f and g are defined by f(x) = 6x + 8; g(x) = `(x - 2)/3`
Write an expression for gf(x) in its simplest form
If a function f(x) is given as f(x) = x2 – 6x + 4 for all x ∈ R, then f(–3) = ______.
Find the domain for which the functions f(x) = 2x2 – 1 and g(x) = 1 – 3x are equal.
Find the domain of the following function.
f(x) = [x] + x
Find the domain of the following functions given by f(x) = `(x^3 - x + 3)/(x^2 - 1)`
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find `(f/g)(x)`
The domain for which the functions defined by f(x) = 3x2 – 1 and g(x) = 3 + x are equal is ______.
The domain of the function f(x) = `sin^-1((|x| + 5)/(x^2 + 1))` is (–∞, –a] ≈ [a, ∞). Then a is equal to ______.
The range of the function y = `1/(2 - sin3x)` is ______.
The function f: R `rightarrow` R defined by f(x) = sin x is ______.
If f: R `rightarrow` R be a function defined by f(x) = 4x3 – 7. Then ______.
The range of the function f(x) = `""^(7 - x)P_(x - 3)` is ______.
