Advertisements
Advertisements
प्रश्न
A ground is in the form of isosceles trapezium with parallel sides measuring 42 m and 36 m long. The distance between the parallel sides is 30 m. Find the cost of levelling it at the rate of ₹ 135 per sq.m
उत्तर
Parallel sides of the trapezium a = 42 m, b = 36 m
Also height h = 30 m
Area of the trapezium = `1/2` × h × (a + b) sq.unit
= `1/2` × 30 × (42 + 36) m2
= `1/2` × 30 × 78 m2
Area = 1,170 m2
Cost of levelling 1 m2 = ₹ 135
∴ Cost of levelling 1170 m2
= ₹ 1170 × ₹ 135
= ₹ 1,57,950
Cost of levelling the ground = ₹ 1,57,950
APPEARS IN
संबंधित प्रश्न
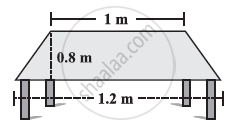
The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.
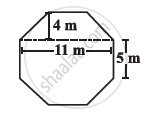
Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
Find the area of a trapezium whose parallel sides of lengths 10 cm and 15 cm are at a distance of 6 cm from each other. Calculate this area as
the sum of the areas of two triangles and one rectangle.
The cross-section of a canal is a trapezium in shape. If the canal is 10 m wide at the top 6 m wide at the bottom and the area of cross-section is 72 m2 determine its depth.
The area of a trapezium is 91 cm2 and its height is 7 cm. If one of the parallel sides is longer than the other by 8 cm, find the two parallel sides.
Mohan wants to buy a trapezium shaped field. Its side along the river is parallel and twice the side along the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.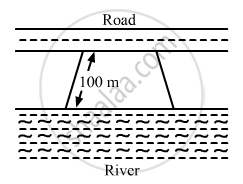
The area of a trapezium is 279 sq.cm and the distance between its two parallel sides is 18 cm. If one of its parallel sides is longer than the other side by 5 cm, find the lengths of its parallel sides.
In a trapezium if the sum of the parallel sides is 10 cm and the area is 140 sq.cm, then the height is
The areas of two circles are in the ratio 49 : 64. Find the ratio of their circumferences.
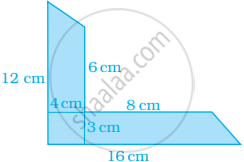
Find the area of the shaded portion in the following figure.