Advertisements
Advertisements
प्रश्न
A long straight wire carrying current of 25 A rests on a table as shown in figure. Another wire PQ of length 1 m, mass 2.5 g carries the same current but in the opposite direction. The wire PQ is free to slide up and down. To what height will PQ rise?
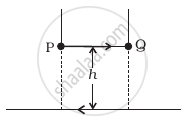
उत्तर
The force is applied on PQ by a long straight wire carrying a current of 25 A which rests on a table. And the forces which other are repulsive if two straight wires are placed parallel to each other carrying current in opposite direction. Now if the wire PQ is in equilibrium then that repulsive force onPQ must balance its weight.
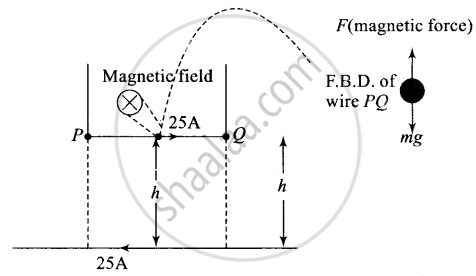
The magnetic field produced by a long straight wire carrying current of 25 A rests on a table on small wire.
`B = (mu_0I)/(2pih)`
The magnetic force on small conductor is `F = BIl sin θ = BIl`
Force applied on PQ balance the weight of small current carrying wire.
`F = mg = (mu_0I^2l)/(2pih)`
`h = (mu_0I^2l)/(2pimg) = (4pi xx 10^-7 xx (25)^2 xx 1)/(2pi xx 2.5 xx 10^-3 xx 9.8) = 51 xx 10^-4 m`
h = 0.51 cm
APPEARS IN
संबंधित प्रश्न
Two long, straight, parallel conductors carry steady currents, I1 and I2, separated by a distance d. If the currents are flowing in the same direction, show how the magnetic field set up in one produces an attractive force on the other? Obtain the expression for this force. Hence, define one ampere.
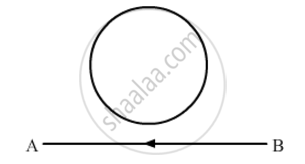
The electric current flowing in a wire in the direction from B to A is decreasing. Find out the direction of the induced current in the metallic loop kept above the wire as shown.
Define one tesla using the expression for the magnetic force acting on a particle of charge q moving with velocity \[\vec{v}\] in a magnetic field \[\vec{B}\] .
Which of the following particles will experience maximum magnetic force (magnitude) when projected with the same velocity perpendicular to a magnetic field?
For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,
B = `(μ_0"IR"^2"N")/(2("x"^2 + "R"^2)^(3/2))`
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by, B = `0.72 (μ_0"NI")/"R"` approximately.
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
Direction of magnetic force on a positive charge moving in a magnetic field is given by ______.
A unit vector is represented as `(0.8hat"i" + "b"hat"j" + 0.4hat"k")`. Hence the value of 'b' must be ______.
With a neat labelled diagram, explain cyclotron motion and cyclotron formula.
What is the relation between Tesla and Gauss?
