Advertisements
Advertisements
प्रश्न
A machine is set to deliver packets of a given weight. Ten samples of size five each were recorded. Below are given relevant data:
| Sample number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| `bar"X"` | 15 | 17 | 15 | 18 | 17 | 14 | 18 | 15 | 1 | 16 |
| R | 7 | 7 | 4 | 9 | 8 | 7 | 12 | 4 | 11 | 5 |
Calculate the control limits for mean chart and the range chart and then comment on the state of control, (conversion factors for n = 5, A2 = 0.58, D3 = 0 and D4 = 2.115)
उत्तर
| Sample number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Tota |
| Mean `(bar"X")` | 15 | 17 | 15 | 18 | 17 | 14 | 18 | 15 | 1 | 16 | `sum"X"` = 162 |
| Range (R) | 7 | 7 | 4 | 9 | 8 | 7 | 12 | 4 | 11 | 5 | `sum"R"` = 74 |
The control limits for `bar"X"` chart is
`\overset{==}{"X"} = (sum"X")/"No. of samples" = 162/10` = 16.2
`bar"R" = (sum"R")/"No. of samples" = 74/10` = 7.4
UCL = `\overset{==}{"X"} + "A"_2+ bar"R"`
= 16.2 + (0.58)(7.4)
= 16.2 + 4.292
= 20.492
= 20.49
CL = `\overset{=}{"X"}` = 16.2
LCL = `\overset{==}{"X"} - "A"_2 bar"R"`
= 16.2 – (0.58)(7.4)
= 16.2 – 4.292
= 11.908
= 11.91
The control limits for Range chart is
CL = `"D"_4bar"R"`
= (2.115)(7.4)
= 15.651
= 15.65
CL = `bar"R"` = 7.4
LCL = `"D"_3 bar"R"` = (0)(7.4) = 0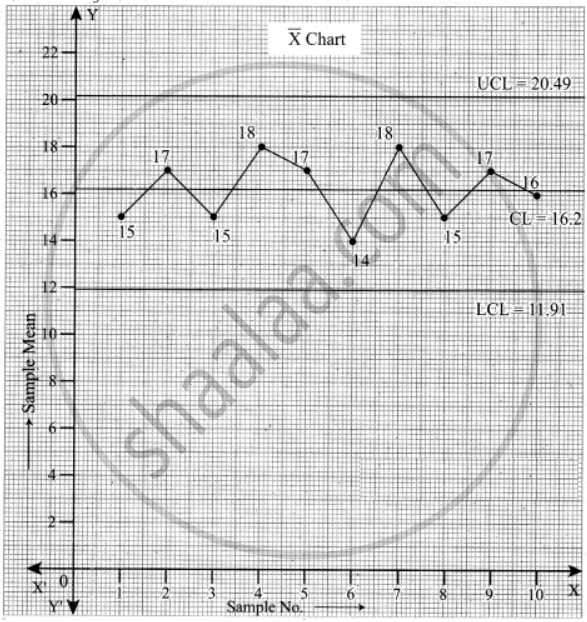
The above diagram shows all the three control lines with the data points plotted.
We see that all the points of the sample mean are within the control limits.
We now draw the R chart for the given data.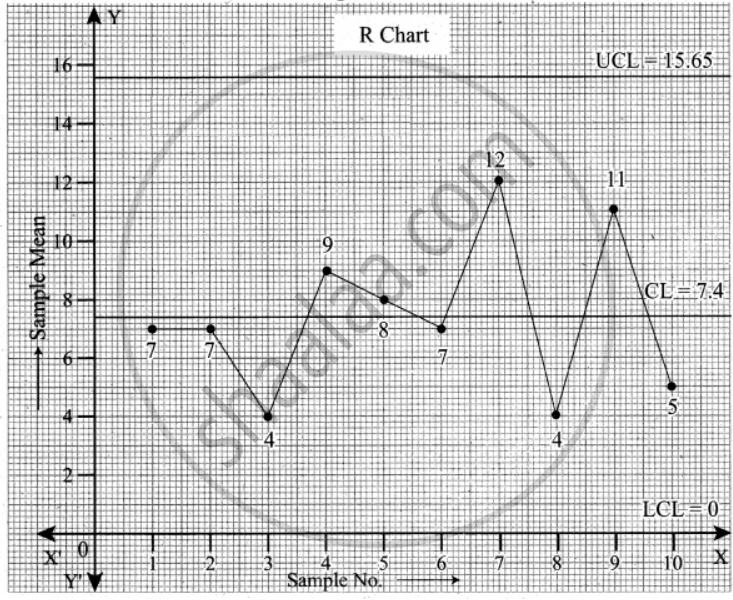
The above diagram shows all the three control lines with the sample range points plotted.
We observe that all the points are within the control limits.
Conclusion: From the above two plots of the sample mean `bar"X"` and sample range R, we conclude that the process is in control.
APPEARS IN
संबंधित प्रश्न
Define assignable cause
Write the control limits for the mean chart
Write the control limits for the R chart
Ten samples each of size five are drawn at regular intervals from a manufacturing process. The sample means `(bar"X")` and their ranges (R) are given below:
| Sample number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| `bar"X"` | 49 | 45 | 48 | 53 | 39 | 47 | 46 | 39 | 51 | 45 |
| R | 7 | 5 | 7 | 9 | 5 | 8 | 8 | 6 | 7 | 6 |
Calculate the control limits in respect of `bar"X"` chart. (Given A2 = 0.58, D3 = 0 and D4 = 2.115) Comment on the state of control
The following data show the values of sample mean `(bar"X")` and its range (R) for the samples of size five each. Calculate the values for control limits for mean, range chart and determine whether the process is in control.
| Sample Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Mean | 11.2 | 11.8 | 10.8 | 11.6 | 11.0 | 9.6 | 10.4 | 9.6 | 10.6 | 10.0 |
| Range | 7 | 4 | 8 | 5 | 7 | 4 | 8 | 4 | 7 | 9 |
(conversion factors for n = 5, A2 = 0.58, D3 = 0 and D4 = 2.115)
A quality control inspector has taken ten ” samples of size four packets each from a potato chips company. The contents of the sample are given below, Calculate the control limits for mean and range chart.
| Sample Number | Observations | |||
| 1 | 2 | 3 | 4 | |
| 1 | 12.5 | 12.3 | 12.6 | 12.7 |
| 2 | 12.8 | 12.4 | 12.4 | 12.8 |
| 3 | 12.1 | 12.6 | 12.5 | 12.4 |
| 4 | 12.2 | 12.6 | 12.5 | 12.3 |
| 5 | 12.4 | 12.5 | 12.5 | 12.5 |
| 6 | 12.3 | 12.4 | 12.6 | 12.6 |
| 7 | 12.6 | 12.7 | 12.5 | 12.8 |
| 8 | 12.4 | 12.3 | 12.6 | 12.5 |
| 9 | 12.6 | 12.5 | 12.3 | 12.6 |
| 10 | 12.1 | 12.7 | 12.5 | 12.8 |
(Given for n = 5, A2 = 0.58, D3 = 0 and D4 = 2.115)
In a production process, eight samples of size 4 are collected and their means and ranges are given below. Construct mean chart and range chart with control limits.
| Samples number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| `bar"X"` | 12 | 13 | 11 | 12 | 14 | 13 | 16 | 15 |
| R | 2 | 5 | 4 | 2 | 3 | 2 | 4 | 3 |
Choose the correct alternative:
R is calculated using
Choose the correct alternative:
The LCL for R chart is given by
The following data gives the average life(in hours) and range of 12 samples of 5lamps each. The data are
| Sample No | 1 | 2 | 3 | 4 | 5 | 6 |
| Sample Mean | 1080 | 1390 | 1460 | 1380 | 1230 | 1370 |
| Sample Range | 410 | 670 | 180 | 320 | 690 | 450 |
| Sample No | 7 | 8 | 9 | 10 | 11 | 12 |
| Sample Mean | 1310 | 1630 | 1580 | 1510 | 1270 | 1200 |
| Sample Range | 380 | 350 | 270 | 660 | 440 | 310 |
Construct control charts for mean and range. Comment on the control limits.
