Advertisements
Advertisements
प्रश्न
A point P with position vector `(- 14hat"i" + 39hat"j" + 28hat"k")/5` divides the line joining A (1, 6, 5) and B in the ratio 3 : 2, then find the point B.
उत्तर
Let A, B and P have position vectors a, b and p respectively.
Then `bar"a" = - hat"i" + 6hat"j" + 5hat"k"`,
`bar"p" = (- 14hat"i" + 39hat"j" + 28hat"k")/5`
Now, P divides AB internally in the ratio 3 : 2
∴ `bar"p" = (3bar"b" + 2bar"a")/5`
∴ `5bar"p" = 3bar"b" + 2bar"a"`
∴ `3bar"b" = 5bar"p" - 2bar"a"`
∴ `3bar"b" = 5((- 14hat"i" + 39hat"j" + 28hat"k")/5) - 2(- hat"i" + 6hat"j" + 5hat"k")`
`= - 14hat"i" + 39hat"j" + 28hat"k" + 2hat"i" - 12hat"j" - 10hat"k"`
`= - 12hat"i" + 27hat"j" + 18hat"k"`
∴ `bar"b" = - 4hat"i" + 9hat"j" + 6hat"k"`
∴ coordinates of B are (-4, 9, 6).
APPEARS IN
संबंधित प्रश्न
If \[\vec{a}\] and \[\vec{b}\] represent two adjacent sides of a parallelogram, then write vectors representing its diagonals.
If a vector makes angles α, β, γ with OX, OY and OZ respectively, then write the value of sin2 α + sin2 β + sin2 γ.
Write the position vector of a point dividing the line segment joining points A and B with position vectors \[\vec{a}\] and \[\vec{b}\] externally in the ratio 1 : 4, where \[\overrightarrow{a} = 2 \hat{i} + 3 \hat{j} + 4 \hat{k} \text{ and }\overrightarrow{b} = - \hat{i} + \hat{j} + \hat{k} .\]
Write the position vector of a point dividing the line segment joining points having position vectors \[\hat{i} + \hat{j} - 2 \hat{k} \text{ and }2 \hat{i} - \hat{j} + 3 \hat{k}\] externally in the ratio 2:3.
If \[\overrightarrow{a} = \hat{i} + 2 \hat{j} - 3 \hat{k} \text{ and }\overrightarrow{b} = 2 \hat{i} + 4 \hat{j} + 9 \hat{k} ,\] find a unit vector parallel to \[\overrightarrow{a} + \overrightarrow{b}\].
Find the position vector of the mid-point of the line segment AB, where A is the point (3, 4, −2) and B is the point (1, 2, 4).
If \[\overrightarrow{a} = x \hat{i} + 2 \hat{j} - z \hat{k}\text{ and }\overrightarrow{b} = 3 \hat{i} - y \hat{j} + \hat{k}\] are two equal vectors, then write the value of x + y + z.
If \[\vec{a} , \vec{b}\] are the vectors forming consecutive sides of a regular hexagon ABCDEF, then the vector representing side CD is
Let G be the centroid of ∆ ABC. If \[\overrightarrow{AB} = \vec{a,} \overrightarrow{AC} = \vec{b,}\] then the bisector \[\overrightarrow{AG} ,\] in terms of \[\vec{a}\text{ and }\vec{b}\] is
If three points A, B and C have position vectors \[\hat{i} + x \hat{j} + 3 \hat{k} , 3 \hat{i} + 4 \hat{j} + 7 \hat{k}\text{ and }y \hat{i} - 2 \hat{j} - 5 \hat{k}\] respectively are collinear, then (x, y) =
If OACB is a parallelogram with \[\overrightarrow{OC} = \vec{a}\text{ and }\overrightarrow{AB} = \vec{b} ,\] then \[\overrightarrow{OA} =\]
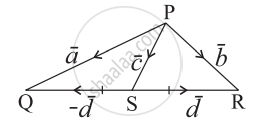
In the given figure express `bar"c"` and `bar"d"` in terms of `bar"a"` and `bar"b"`.
If `|bara|` = 3, `|barb|` = 5, `|barc|` = 7 and `bara + barb + barc = bar0`, then the angle between `bara` and `barb` is ______.
Select the correct option from the given alternatives:
Let α, β, γ be distinct real numbers. The points with position vectors `alphahat"i" + betahat"j" + gammahat"k", betahat"i" + gammahat"j" + alphahat"k", gammahat"i" + alphahat"j" + betahat"k"`
Select the correct option from the given alternatives:
The value of `hat"i".(hat"j" xx hat"k") + hat"j".(hat"i" xx hat"k") + hat"k".(hat"i" xx hat"j")` is
Find the component form of `bar"a"` if it lies in YZ-plane makes 60° with positive Y-axis and `|bar"a"| = 4`.
Two sides of a parallelogram are `3hat"i" + 4hat"j" - 5hat"k"` and `-2hat"j" + 7hat"k"`. Find the unit vectors parallel to the diagonals.
If a parallelogram is constructed on the vectors `bar"a" = 3bar"p" - bar"q", bar"b" = bar"p" + 3bar"q" and |bar"p"| = |bar"q"| = 2` and angle between `bar"p" and bar"q"` is `pi/3,` and angle between lengths of the sides is `sqrt7 : sqrt13`.
Find the acute angle between the curves at their points of intersection, y = x2, y = x3.
Express `hat"i" + 4hat"j" - 4hat"k"` as the linear combination of the vectors `2hat"i" - hat"j" + 3hat"k", hat"i" - 2hat"j" + 4hat"k"` and `- hat"i" + 3hat"j" - 5hat"k"`.
Find the angle between the lines whose direction cosines are given by the equations 6mn - 2nl + 5lm = 0, 3l + m + 5n = 0.
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b" xx bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b".bar"c")`
State whether the expression is meaningful. If not, explain why? If so, state whether it is a vector or a scalar:
`bar"a".(bar"b" + bar"c")`
For any vectors `bar"a", bar"b", bar"c"` show that `(bar"a" + bar"b" + bar"c") xx bar"c" + (bar"a" + bar"b" + bar"c") xx bar"b" + (bar"b" - bar"c") xx bar"a" = 2bar"a" xx bar"c"`
a and b are non-collinear vectors. If p = (2x + 1) a - band q = (x - 2)a +b are collinear vectors, then x = ______.
For 0 < θ < π, if A = `[(costheta, -sintheta), (sintheta, costheta)]`, then ______
The vector with initial point P (2, –3, 5) and terminal point Q(3, –4, 7) is ______.
If `|vec"a"|` = 3 and –1 ≤ k ≤ 2, then `|"k"vec"a"|` lies in the interval ______.
Find the unit vector in the direction of the sum of the vectors `vec"a" = 2hat"i" - hat"j" + hat"k"` and `vec"b" = 2hat"j" + hat"k"`.
If `vec"a" = hat"i" + hat"j" + 2hat"k"` and `hat"b" = 2hat"i" + hat"j" - 2hat"k"`, find the unit vector in the direction of `2vec"a" - vec"b"`
If `vec"a", vec"b", vec"c"` determine the vertices of a triangle, show that `1/2[vec"b" xx vec"c" + vec"c" xx vec"a" + vec"a" xx vec"b"]` gives the vector area of the triangle. Hence deduce the condition that the three points `vec"a", vec"b", vec"c"` are collinear. Also find the unit vector normal to the plane of the triangle.
If `vec"a"` and `vec"b"` are adjacent sides of a rhombus, then `vec"a" * vec"b"` = 0
Classify the following measures as scalar and vector.
10-19 coulomb
Classify the following as scalar and vector quantity.
Velocity
If `veca ≠ vec(0), veca.vecb = veca.vecc, veca xx vecb = veca xx vecc`, then show that `vecb = vecc`.
Check whether the vectors `2 hati + 2 hatj + 3 hatk, -3 hati + 3 hatj + 2 hatk "and" 3 hati + 4 hatk` from a triangle or not.
Check whether the vectors `2hati + 2hatj + 3hat k, -3hati + 3hatj + 2hat k` and `3hati + 4hatk` form a triangle or not.
Check whether the vectors `2hati+2hatj+3hatk,-3hati+3hatj+2hatk` and `3hati+4hatk` form a triangle or not.
Check whether the vectors `2hati + 2hatj + 3hatk, -3hati + 3hatj + 2hatk and 3hati + 4hatk` form a triangle or not.
