Advertisements
Advertisements
प्रश्न
A rectangular cardboard sheet has length 32 cm and breadth 26 cm. Squares each of side 3 cm, are cut from the corners of the sheet and the sides are folded to make a rectangular container. Find the capacity of the container formed.
उत्तर

Length of sheet = 32 cm
Breadth of sheet = 26 cm
Side of each square = 3cm
∴ Inner length = 32 - 2 x 3 = 32 - 6 = 26 cm
Inner breadth = 26 - 2 x 3 = 26 - 6 = 20 cm
By folding the sheet, the length of the container = 26 cm
Breadth of the container = 20 cm and height of the container = 3 cm
∴ Vol. of the container = l x b x h
= 26 cm x 20 cm x 3 cm = 1560 cm3
APPEARS IN
संबंधित प्रश्न
The following figure shows a solid of uniform cross-section. Find the volume of the solid. All measurements are in centimeters.
Assume that all angles in the figures are right angles.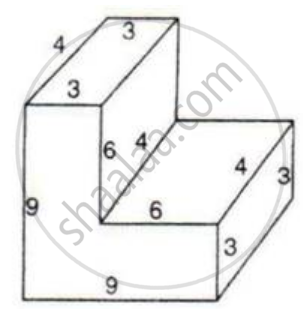
A swimming pool is 40 m long and 15 m wide. Its shallow and deep ends are 1.5 m and 3 m deep respectively. If the bottom of the pool slopes uniformly, find the amount of water in liters required to fill the pool.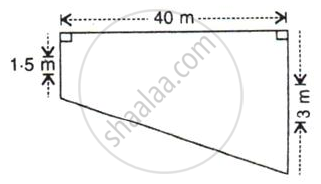
The following figure shows a closed victory-stand whose dimensions are given in cm.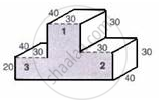
Find the volume and the surface area of the victory stand.
A school auditorium is 40 m long, 30 m broad and 12 m high. If each student requires 1.2 m2 of the floor area; find the maximum number of students that can be accommodated in this auditorium. Also, find the volume of air available in the auditorium, for each student.
The figure represents the cross section of a swimming pool 10 m broad, 2 m deep at one end, 3 m deep at the other end. Calculate the volume of water it will hold when full, given that its length is 40 m.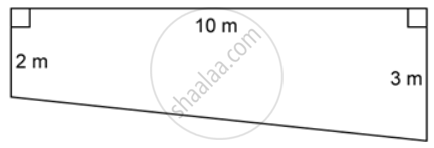
A swimming pool is 50 m long and 15 m wide. Its shallow and deep ends are 1.5 m and 4.5 m respectively. If the bottom of the pool slopes uniformly, find the amount of water in kilolitres required to fill the pool (1 m3 = 1000 liters).
The figure shows the cross section of 0.2 m a concrete wall to be constructed. It is 0.2 m wide at the top, 2.0 m wide at the bottom and its height is 4.0 m, and its length is 40 m. Calculate the cross sectional area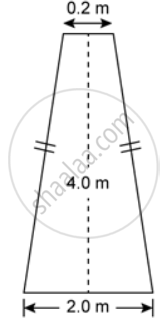
The cross section of a swimming pool is a trapezium whose shallow and deep ends are 1 m and 3 m respectively. If the length of the pool is 50 m and its width is 1.5 m, calculate the volume of water it holds.
A hose-pipe of cross section area 3 cm2 delivers 1800 liters of water in 10 minutes. Find the speed of water in km/h through the pipe.
The cross section of a canal is a trapezium with the base length of 3 m and the top length of 5 m. It is 2 m deep and 400 m long. Calculate the volume of water it holds.
