Advertisements
Advertisements
प्रश्न
A string is wrapped over the edge of a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
उत्तर
Let the radius of the disc be R.
Let the tension in the string be T.
Let the acceleration of the disc be a.

From the free body diagram, we have
\[mg - T = ma ........(1)\]
Torque about the centre of disc,
\[T \times R = I \times \alpha\]
\[\Rightarrow T \times R = \frac{1}{2}m R^2 \times \frac{a}{R}\]
\[ \Rightarrow T = \frac{1}{2}ma ...........(2)\]
Putting this value in equation (1), we get
\[mg - \frac{1}{2}ma = ma\]
\[ \Rightarrow mg = \frac{3}{2}ma\]
\[ \Rightarrow a = \frac{2g}{3}\]
APPEARS IN
संबंधित प्रश्न
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. (a) Will it reach the bottom with the same speed in each case? (b) Will it take longer to roll down one plane than the other? (c) If so, which one and why?
Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height h is given by `v^2 = (2gh)/((1+k^2"/"R^2))`.
Using dynamical consideration (i.e. by consideration of forces and torques). Note k is the radius of gyration of the body about its symmetry axis, and R is the radius of the body. The body starts from rest at the top of the plane.
Read each statement below carefully, and state, with reasons, if it is true or false;
The instantaneous speed of the point of contact during rolling is zero.
In rear-wheel drive cars, the engine rotates the rear wheels and the front wheels rotate only because the car moves. If such a car accelerates on a horizontal road the friction
(a) on the rear wheels is in the forward direction
(b) on the front wheels is in the backward direction
(c) on the rear wheels has larger magnitude than the friction on the front wheels
(d) on the car is in the backward direction.
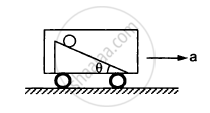
The following figure shows a smooth inclined plane fixed in a car accelerating on a horizontal road. The angle of incline θ is related to the acceleration a of the car as a = g tanθ. If the sphere is set in pure rolling on the incline, _____________.
A cylinder rolls on a horizontal place surface. If the speed of the centre is 25 m/s, what is the speed of the highest point?
Answer in Brief:
A rigid object is rolling down an inclined plane derive the expression for the acceleration along the track and the speed after falling through a certain vertical distance.
What is the condition for pure rolling?
A solid sphere rolls down from top of inclined plane, 7m high, without slipping. Its linear speed at the foot of plane is ______. (g = 10 m/s2)
A solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with velocity of 10 emfs. The total kinetic energy of sphere is ______.
The angular velocity of minute hand of a clock in degree per second is ______.
An object is rolling without slipping on a horizontal surface and its rotational kinetic energy is two-thirds of translational kinetic energy. The body is ______.
If x = at + bt2, where x is the distance travelled by the body in kilometers while t is the time in seconds, then the unit of b is ______.
A solid sphere of mass 2 kg is rolling on a frictionless horizontal surface with velocity 6m/s. It collides on the free end of an ideal spring whose other end is fixed. The maximum compression produced in the spring will be ______.
(Force constant of the spring = 36 N/m)
The kinetic energy and angular momentum of a body rotating with constant angular velocity are E and L. What does `(2E)/L` represent?
The angular displacement of a particle in 6 sec on a circle with angular velocity `pi/3` rad/sec is ______.
When a sphere rolls without slipping, the ratio of its kinetic energy of translation to its total kinetic energy is ______.
A disc of mass 4 kg rolls on a horizontal surface. If its linear speed is 3 m/ s, what is its total kinetic energy?
