Advertisements
Advertisements
प्रश्न
A wire AB is carrying a steady current of 10 A and is lying on the table. Another wire CD carrying 6 A is held directly above AB at a height of 2 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g = 10 ms−2]
उत्तर
Force per unit length between the current carrying wires is given as:
`F = (μ_0)/(4pi) (2I_1I_2)/r `,where I1 = current in wire AB = 10 A and I2 = current in wire CD = 6 A`
r = distance between wires = 2 mm = 2 × 10-3 m.
Let m be the mass per unit length of wire CD. As the force balances the weight of the wire
`therefore (μ_0)/(4pi) (2I_1I_2)/r = mg => 10^-7 xx (2xx10xx6)/(2xx10^-3) = m xx 10`
`therefore m = 10^-7 xx (2 xx 10 xx xx 6)/(2 xx 10^-3) xx 1/10 = 6 xx 10^-4 kg \ m^-1`
APPEARS IN
संबंधित प्रश्न
Derive an expression for the mutual inductance of two long co-axial solenoids of same length wound one over the other,
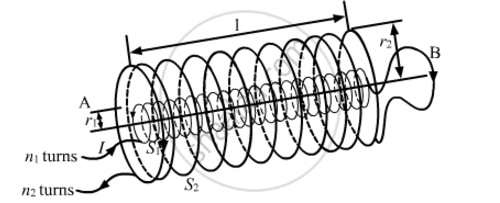
Two long coaxial insulated solenoids, S1 and S2 of equal lengths are wound one over the other as shown in the figure. A steady current "I" flow thought the inner solenoid S1 to the other end B, which is connected to the outer solenoid S2 through which the same current "I" flows in the opposite direction so as to come out at end A. If n1 and n2 are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point (i) inside on the axis and (ii) outside the combined system
Define the term self-inductance of a solenoid.
In what respect is a toroid different from a solenoid?
How is the magnetic field inside a given solenoid made strong?
A tightly-wound solenoid of radius a and length l has n turns per unit length. It carries an electric current i. Consider a length dx of the solenoid at a distance x from one end. This contains n dx turns and may be approximated as a circular current i n dx. (a) Write the magnetic field at the centre of the solenoid due to this circular current. Integrate this expression under proper limits to find the magnetic field at the centre of the solenoid. (b) verify that if l >> a, the field tends to B = µ0ni and if a >> l, the field tends to `B =(mu_0nil)/(2a)` . Interpret these results.
A capacitor of capacitance 100 µF is connected to a battery of 20 volts for a long time and then disconnected from it. It is now connected across a long solenoid having 4000 turns per metre. It is found that the potential difference across the capacitor drops to 90% of its maximum value in 2.0 seconds. Estimate the average magnetic field produced at the centre of the solenoid during this period.
A current of 1.0 A is established in a tightly wound solenoid of radius 2 cm having 1000 turns/metre. Find the magnetic energy stored in each metre of the solenoid.
A long solenoid carrying a current produces a magnetic field B along its axis. If the current is doubled and the number of turns per cm is halved, the new value of magnetic field will be equal to ______.
