Advertisements
Advertisements
प्रश्न
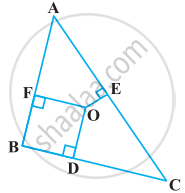
आकृति में ∆ABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD ⊥ BC, OE ⊥ AC और OF ⊥ AB है। दर्शाइए कि
- OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
- AF2 + OB2 + CE2 = AE2 + CD2 + BF2
उत्तर
दिया है: ∆ABC के अभ्यंतर में स्थित कोई बिन्दु O तथा
OD ⊥ BC, OE ⊥ CA, OF ⊥ AB
रचना: OA, OB और OC को मिलाइए।
(i) ∵ पाइथागोरस प्रमेय से,
समकोण ∆OFA में,
OA2 – OF2 = AF2 …(1)
समकोण ∆ODB में,
OB2 – OD2 = BD2 ….(2)
एवं समकोण ∆OEC में,
OC2 – OE2 = CE2 …(3)
OA2 – OF2 + OB2 – OD2 + OC2 – OE2 = AF2 + BD2 + CE2
[समीकरण (1) + (2) + (3) से]
OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2 …(4)
इति सिद्धम्
(ii) चूँकि पाइथागोरस प्रमेय से,
समकोण ∆OEA में,
OA2 – OE2 = AE2 ….(5)
समकोण ∆OFB में,
OB2 – OF2 = BF2 ….(6)
एवं समकोण ∆ODC में,
OC2 – OD2 = CD2 ….(7)
OA2 – OE2 + OB2 – OF2 + OC2 – OD2 = AE2 + BF2 + CD2
[समीकरण (5) + (6) + (7) से]
OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AE2 + CD2 + BF2 …(8)
AF2 + BD2 + CE2 = AE2 + CD2 + BF2
[समीकरण (4) एवं (8) से]
इति सिद्धम्
APPEARS IN
संबंधित प्रश्न
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
3 cm, 8 cm, 6 cm
आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि
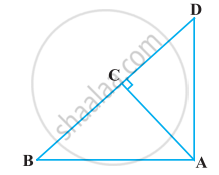
AB2 = BC.BD
आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि

AD2 = BD.CD
एक समबाहु त्रिभुज ABC की भुजा 2a है। उसके प्रत्येक शीर्षलंब की लंबाई ज्ञात कीजिए।
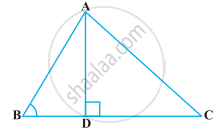
आकृति में ABC एक त्रिभुज है जिसमें ∠ABC < 90° हैं तथा AD ⊥ BC है। सिद्ध कीजिए कि AC2 = AB2 + BC2 – 2BC.BD है।
10 m लंबी एक सीढ़ी, जो एक उर्ध्वाधर दीवार के सहारे टिकी हुई है, के निचले सिरे की दीवार के आधार से दूरी 6 m है। दीवार पर उस बिंदु की ऊँचाई ज्ञात कीजिए, जहाँ तक सीढ़ी का ऊपरी सिरा पहुँचता है।
∆PQR में, PD ⊥ QR इस प्रकार है कि D भुजा QR पर स्थित है। यदि PQ = a, PR = b, QD = c और DR = d है, तो सिद्ध कीजिए कि (a + b)(a – b) = (c + d)(c – d) है।
किसी चतुर्भुज ABCD में, ∠A + ∠D = 90° है। सिद्ध कीजिए कि AC2 + BD2 = AD2 + BC2 है।
[संकेत : AB और DC को E पर मिलने के लिए बढ़ाइए]।
सिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण पर खींचे गए अर्धवृत्त का क्षेत्रफल अन्य दो भुजाओं पर खींचे गए अर्धवृत्तों के क्षेत्रफलों के योग के बराबर होता है।
सिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण पर खींचे गए समबाहु त्रिभुज का क्षेत्रफल अन्य दो भुजाओं पर खींचे गए समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होता है।
