Advertisements
Advertisements
Question
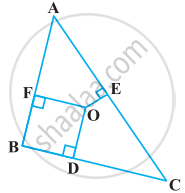
आकृति में ∆ABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD ⊥ BC, OE ⊥ AC और OF ⊥ AB है। दर्शाइए कि
- OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
- AF2 + OB2 + CE2 = AE2 + CD2 + BF2
Advertisements
Solution
दिया है: ∆ABC के अभ्यंतर में स्थित कोई बिन्दु O तथा
OD ⊥ BC, OE ⊥ CA, OF ⊥ AB
रचना: OA, OB और OC को मिलाइए।
(i) ∵ पाइथागोरस प्रमेय से,
समकोण ∆OFA में,
OA2 – OF2 = AF2 …(1)
समकोण ∆ODB में,
OB2 – OD2 = BD2 ….(2)
एवं समकोण ∆OEC में,
OC2 – OE2 = CE2 …(3)
OA2 – OF2 + OB2 – OD2 + OC2 – OE2 = AF2 + BD2 + CE2
[समीकरण (1) + (2) + (3) से]
OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2 …(4)
इति सिद्धम्
(ii) चूँकि पाइथागोरस प्रमेय से,
समकोण ∆OEA में,
OA2 – OE2 = AE2 ….(5)
समकोण ∆OFB में,
OB2 – OF2 = BF2 ….(6)
एवं समकोण ∆ODC में,
OC2 – OD2 = CD2 ….(7)
OA2 – OE2 + OB2 – OF2 + OC2 – OD2 = AE2 + BF2 + CD2
[समीकरण (5) + (6) + (7) से]
OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AE2 + CD2 + BF2 …(8)
AF2 + BD2 + CE2 = AE2 + CD2 + BF2
[समीकरण (4) एवं (8) से]
इति सिद्धम्
RELATED QUESTIONS
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
7 cm, 24 cm, 25 cm
आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि
AC2 = BC.DC
ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है। सिद्ध कीजिए कि AB2 = 2AC2 है।
18 m ऊंचे एक ऊर्ध्वाधर खंभे के ऊपरी सिरे से एक तार का एक सिरा जुड़ा हुआ है तथा तार का दूसरा सिरा एक खूँटे से जुड़ा हुआ है। खंभे के आधार से खूँटे को कितनी दूरी पर गाड़ा जाए कि तार तना रहे जबकि तार की लंबाई 24 m है।
किसी त्रिभुज ABC के शीर्ष A से BC पर डाला गया लम्ब BC को बिंदु D पर इस प्रकार प्रतिच्छेद करता है कि DB = 3CD है (देखिए आकृति) सिद्ध कीजिए कि 2AB2 = 2AC2 + BC2 है।
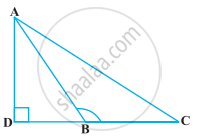
आकृति में ABC एक त्रिभुज है जिसमें ∠ABC > 90° हैं तथा AD ⊥ CB है। सिद्ध कीजिए कि AC2 = AB2 + BC2 + 2 BC.BD है।
आकृति में ABC एक त्रिभुज है जिसमें ∠ABC < 90° हैं तथा AD ⊥ BC है। सिद्ध कीजिए कि AC2 = AB2 + BC2 – 2BC.BD है।
आकृति में AD त्रिभुज ABC की एक माध्यिका है तथा AM ⊥ BC है। सिद्ध कीजिए कि
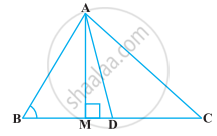
(i) AC2 = AD2 + BC.DM + `("BC"/2)^2`
(ii) AB2 = AD2 – BC.DM + `("BC"/2)^2`
(ii) AC2 + AB2 = 2AD2 + `1/2` BC2
क्या भुजाओं 25 cm, 5 cm और 24 cm वाला त्रिभुज एक समकोण त्रिभुज है? अपने उत्तर के लिए कारण दीजिए।
सिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण पर खींचे गए समबाहु त्रिभुज का क्षेत्रफल अन्य दो भुजाओं पर खींचे गए समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होता है।
