Advertisements
Advertisements
Question
सिद्ध कीजिए कि एक समचतुर्भुज की भुजाओं के वर्गों का योग उसके विकर्णों के वर्गों के योग के बराबर होता है।
Solution
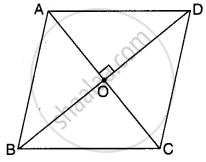
मान लीजिए ABCD एक समचतुर्भुज है, जिसके विकर्ण AC और BD परस्पर बिन्दु O पर प्रतिच्छेद करते हैं। हम जानते हैं कि समचतुर्भुज की चारों भुजाएँ बराबर होती हैं तथा उसके विकर्ण परस्पर एक-दूसरे को समकोण पर समद्विभाजित करते हैं एवं समचतुर्भुज को चार सर्वांगसम समकोण त्रिभुजों में बाँटते हैं।
अब समकोण त्रिभुज AOB में, ∠AOB = 90°
⇒ AB2 = AO2 + BO2 [पाइथागोरस प्रमेय से]
= `("AC"/2)^2 + ("BD"/2)^2`
[∵ AO = `1/2` AC एवं BO = `1/2` BD]
⇒ AB2 = `1/4`AC2 + `1/4`BD2
⇒ 4AB2 = AC2 + BD2
⇒ AB2 + BC2 + CD2 + DA2 = AC2 + BD2 [∵ AB = BC = CD = DA]
अतः एक समचतुर्भुज की भुजाओं के वर्गों का योग उसके विकर्णों के वर्गों के योग के बराबर होता है।
इति सिद्धम्
APPEARS IN
RELATED QUESTIONS
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
3 cm, 8 cm, 6 cm
एक समबाहु त्रिभुज ABC की भुजा 2a है। उसके प्रत्येक शीर्षलंब की लंबाई ज्ञात कीजिए।
दो खंभे जिनकी ऊँचाइयाँ 6 m और 11 m हैं तथा ये समतल भूमि पर खड़े हैं। यदि इनके पाद बिंदुओं के बीच की दूरी 12 m है तो इनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।
किसी समबाहु त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि BD = `1/3` BC है। सिद्ध कीजिए कि 9AD2 = 7AB2 है।
किसी समबाहु त्रिभुज में, सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्षलंब के वर्ग के चार गुने के बराबर होता है।
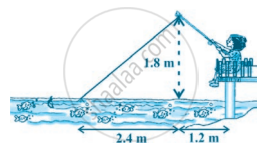
नाज़िमा एक नदी की धारा में मछलियाँ पकड़ रही है। उसकी मछली पकड़ने वाली छड़ का सिरा पानी की सतह से 1.8 m ऊपर है तथा डोरी के निचले सिरे से लगा काँटा पानी के सतह पर इस प्रकार स्थित है कि उसकी नाज़िमा से दूरी 3.6 m है और छड़ के सिरे के ठीक नीचे पानी के सतह पर स्थित बिंदु से उसकी दूरी 2.4 m है। यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से काँटे तक) तनी हुई है, उसने कितनी डोरी बाहर निकाली हुई है (देखिए आकृति)? यदि वह डोरी को 5 cm/s की दर से अंदर खींचे, तो 12 सेकंड के बाद नाज़िमा की काँटे से क्षैतिज दूरी कितनी होगी?
क्या भुजाओं 25 cm, 5 cm और 24 cm वाला त्रिभुज एक समकोण त्रिभुज है? अपने उत्तर के लिए कारण दीजिए।
भुजा 8 cm वाले एक समबाहु त्रिभुज का शीर्षलंब ज्ञात कीजिए।
∆PQR में, PD ⊥ QR इस प्रकार है कि D भुजा QR पर स्थित है। यदि PQ = a, PR = b, QD = c और DR = d है, तो सिद्ध कीजिए कि (a + b)(a – b) = (c + d)(c – d) है।
किसी चतुर्भुज ABCD में, ∠A + ∠D = 90° है। सिद्ध कीजिए कि AC2 + BD2 = AD2 + BC2 है।
[संकेत : AB और DC को E पर मिलने के लिए बढ़ाइए]।
