Advertisements
Advertisements
Question
किसी समबाहु त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि BD = `1/3` BC है। सिद्ध कीजिए कि 9AD2 = 7AB2 है।
Solution
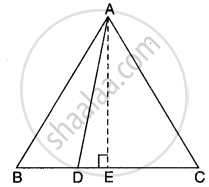
दिया है: ∆ABC एक समबाहु त्रिभुज जिसकी भुजा BC पर बिन्दु D इस प्रकार स्थित है कि BD = `1/3` BC
यहाँ AB = BC = CA ….(1)
एवं BD = `1/3` BC …(2)
रचना: A से AE ⊥ BC खींचिए।
चूँकि BE = EC = `1/2` BC = `1/2` AB …(3) [∵ BC = AB]
[∵ समबाहु त्रिभुज का शीर्ष लम्ब आधार को समाद्विभाजित करता है।]
⇒ DE = BE – BD = `"BC"/2 − "BC"/3` [समीकरण (3) एवं (2) से]
DE = `(3"BC" − 2"BC")/6 = "BC"/6 = "AB"/6` …..(4) [∵ BC = AB]
∵ समकोण ∆AEB में, ∠AEB समकोण है।
⇒ AE2 = AB2 – BE2 ….(5)
∵ समकोण ∆AED में, ∠AED समकोण है
⇒ AE2 = AD2 – DE2 …(6)
⇒ AB2 – BE2 = AD2 – DE2 …..(7) [समीकरण (5) एवं (6) से]
⇒ `"AB"^2 - ("AB"/2)^2 = "AD"^2 - ("AB"/6)^2`
⇒ `"AB"^2 - "AB"^2/4 = "AD"^2 - "AB"^2/36` [समीकरण (3), (4) एवं (7) से]
⇒ 36AB2 – 9AB2 = 36AD2 – AB2
⇒ 36AD2 = 36AB2 + AB2 – 9AB2 = 28AB2
⇒ 9AD2 = 7AB2
इति सिद्धम्
APPEARS IN
RELATED QUESTIONS
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
3 cm, 8 cm, 6 cm
एक त्रिभुज ABC जिसका कोण C समकोण है, की भुजाओं CA और CB पर क्रमशः बिंदु D और E स्थित हैं। सिद्ध कीजिए कि AE2 + BD2 = AB2 + DE2 है।
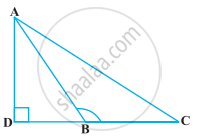
आकृति में ABC एक त्रिभुज है जिसमें ∠ABC > 90° हैं तथा AD ⊥ CB है। सिद्ध कीजिए कि AC2 = AB2 + BC2 + 2 BC.BD है।
आकृति में AD त्रिभुज ABC की एक माध्यिका है तथा AM ⊥ BC है। सिद्ध कीजिए कि
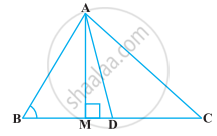
(i) AC2 = AD2 + BC.DM + `("BC"/2)^2`
(ii) AB2 = AD2 – BC.DM + `("BC"/2)^2`
(ii) AC2 + AB2 = 2AD2 + `1/2` BC2
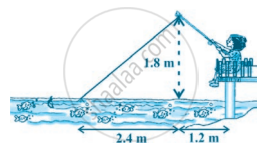
नाज़िमा एक नदी की धारा में मछलियाँ पकड़ रही है। उसकी मछली पकड़ने वाली छड़ का सिरा पानी की सतह से 1.8 m ऊपर है तथा डोरी के निचले सिरे से लगा काँटा पानी के सतह पर इस प्रकार स्थित है कि उसकी नाज़िमा से दूरी 3.6 m है और छड़ के सिरे के ठीक नीचे पानी के सतह पर स्थित बिंदु से उसकी दूरी 2.4 m है। यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से काँटे तक) तनी हुई है, उसने कितनी डोरी बाहर निकाली हुई है (देखिए आकृति)? यदि वह डोरी को 5 cm/s की दर से अंदर खींचे, तो 12 सेकंड के बाद नाज़िमा की काँटे से क्षैतिज दूरी कितनी होगी?
यदि ∆PQR की एक भुजा PQ पर S एक ऐसा बिंदु है कि PS = QS = RS है, तो ______।
∆PQR में, PD ⊥ QR इस प्रकार है कि D भुजा QR पर स्थित है। यदि PQ = a, PR = b, QD = c और DR = d है, तो सिद्ध कीजिए कि (a + b)(a – b) = (c + d)(c – d) है।
एक समलंब ABCD, जिसमें AB || DC है, के विकर्णों AC और BD का प्रतिच्छेद बिंदु O है। O से होकर एक रेखाखंड PQ भुजा AB के समांतर खींचा गया है, जो AD को P और BC को Q पर मिलता है। सिद्ध कीजिए कि PO = QO है।
आकृति में, रेखाखंड DF त्रिभुज ABC की भुजा AC को बिंदु E पर इस प्रकार प्रतिच्छेद करता है कि E, भुजा AC का मध्य-बिंदु है और ∠AEF = ∠AFE है। सिद्ध कीजिए कि `(BD)/(CD) = (BF)/(CE)` है।

सिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण पर खींचे गए समबाहु त्रिभुज का क्षेत्रफल अन्य दो भुजाओं पर खींचे गए समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होता है।
