Advertisements
Advertisements
Question
सिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण पर खींचे गए समबाहु त्रिभुज का क्षेत्रफल अन्य दो भुजाओं पर खींचे गए समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होता है।
Solution

माना एक समकोण त्रिभुज BAC है जिसमें ∠A समकोण है और AC = y, AB = x है।
ΔABC की तीन भुजाओं पर तीन समबाहु त्रिभुज ΔAEC, ΔAFB और ΔCBD खींचे गए हैं।
पुनः माना कि AC, AS और BC पर बने त्रिभुजों का क्षेत्रफल क्रमशः A1, A2 और A3 है।
साबित करने के लिए: A3 = A1 + A2
प्रमाण: ΔCAB में,
पाइथागोरस प्रमेय द्वारा,
BC2 = AC2 + AB2
⇒ BC2 = y2 + x2
⇒ BC = `sqrt(y^2 + x^2)`
हम जानते हैं कि,
एक समबाहु त्रिभुज का क्षेत्रफल = `sqrt(3)/4` (भुजा)2
∴ समबाहु ΔAEC का क्षेत्रफल,
A1 = `sqrt(3)/4 ("AC")^2`
⇒ A1 = `sqrt(3)/4 y^2` ...(i)
और समबाहु ΔAFB का क्षेत्रफल,
A2 = `sqrt(3)/4 ("AB")^2`
= `(sqrt(3)x^2)/4` ...(ii)
और समबाहु ΔCBD का क्षेत्रफल,
A3 = `sqrt(3)/4 ("CB")^2`
= `sqrt(3)/4 (y^2 + x^2)`
= `sqrt(3)/4 y^2 + sqrt(3)/4 x^2`
= A1 + A2 ...[समीकरण (i) और (ii) से]
⇒ A3 = A1 + A2
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
7 cm, 24 cm, 25 cm
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
3 cm, 8 cm, 6 cm
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
13 cm, 12 cm, 5 cm
आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि
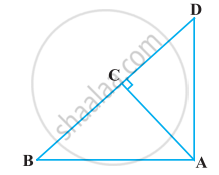
AB2 = BC.BD
आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि

AC2 = BC.DC
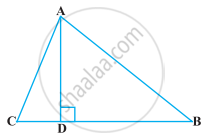
किसी त्रिभुज ABC के शीर्ष A से BC पर डाला गया लम्ब BC को बिंदु D पर इस प्रकार प्रतिच्छेद करता है कि DB = 3CD है (देखिए आकृति) सिद्ध कीजिए कि 2AB2 = 2AC2 + BC2 है।
किसी समबाहु त्रिभुज में, सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्षलंब के वर्ग के चार गुने के बराबर होता है।
सही उत्तर चुनकर उसका औचित्य दीजिए: ∆ABC में, AB = `6sqrt3` cm, AC = 12 cm और BC = 6 cm है। कोण B है: ______
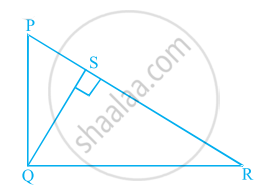
आकृति में PQR एक समकोण त्रिभुज है, जिसका ∠Q समकोण है तथा QS ⊥ PR है। यदि PQ = 6 cm और PS = 4 cm है, तो QS, RS और QR ज्ञात कीजिए।
एक समलंब ABCD, जिसमें AB || DC है, के विकर्णों AC और BD का प्रतिच्छेद बिंदु O है। O से होकर एक रेखाखंड PQ भुजा AB के समांतर खींचा गया है, जो AD को P और BC को Q पर मिलता है। सिद्ध कीजिए कि PO = QO है।
