Advertisements
Advertisements
प्रश्न
सिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण पर खींचे गए समबाहु त्रिभुज का क्षेत्रफल अन्य दो भुजाओं पर खींचे गए समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होता है।
उत्तर

माना एक समकोण त्रिभुज BAC है जिसमें ∠A समकोण है और AC = y, AB = x है।
ΔABC की तीन भुजाओं पर तीन समबाहु त्रिभुज ΔAEC, ΔAFB और ΔCBD खींचे गए हैं।
पुनः माना कि AC, AS और BC पर बने त्रिभुजों का क्षेत्रफल क्रमशः A1, A2 और A3 है।
साबित करने के लिए: A3 = A1 + A2
प्रमाण: ΔCAB में,
पाइथागोरस प्रमेय द्वारा,
BC2 = AC2 + AB2
⇒ BC2 = y2 + x2
⇒ BC = `sqrt(y^2 + x^2)`
हम जानते हैं कि,
एक समबाहु त्रिभुज का क्षेत्रफल = `sqrt(3)/4` (भुजा)2
∴ समबाहु ΔAEC का क्षेत्रफल,
A1 = `sqrt(3)/4 ("AC")^2`
⇒ A1 = `sqrt(3)/4 y^2` ...(i)
और समबाहु ΔAFB का क्षेत्रफल,
A2 = `sqrt(3)/4 ("AB")^2`
= `(sqrt(3)x^2)/4` ...(ii)
और समबाहु ΔCBD का क्षेत्रफल,
A3 = `sqrt(3)/4 ("CB")^2`
= `sqrt(3)/4 (y^2 + x^2)`
= `sqrt(3)/4 y^2 + sqrt(3)/4 x^2`
= A1 + A2 ...[समीकरण (i) और (ii) से]
⇒ A3 = A1 + A2
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
50 cm, 80 cm, 100 cm
आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि
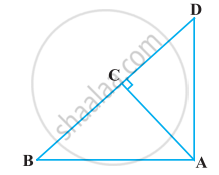
AC2 = BC.DC
आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि

AD2 = BD.CD
सिद्ध कीजिए कि एक समचतुर्भुज की भुजाओं के वर्गों का योग उसके विकर्णों के वर्गों के योग के बराबर होता है।
किसी त्रिभुज ABC के शीर्ष A से BC पर डाला गया लम्ब BC को बिंदु D पर इस प्रकार प्रतिच्छेद करता है कि DB = 3CD है (देखिए आकृति) सिद्ध कीजिए कि 2AB2 = 2AC2 + BC2 है।
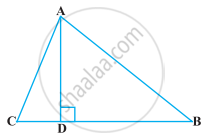
किसी समबाहु त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि BD = `1/3` BC है। सिद्ध कीजिए कि 9AD2 = 7AB2 है।
आकृति में ABC एक त्रिभुज है जिसमें ∠ABC > 90° हैं तथा AD ⊥ CB है। सिद्ध कीजिए कि AC2 = AB2 + BC2 + 2 BC.BD है।
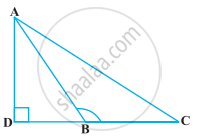
आकृति में ABC एक त्रिभुज है जिसमें ∠ABC < 90° हैं तथा AD ⊥ BC है। सिद्ध कीजिए कि AC2 = AB2 + BC2 – 2BC.BD है।
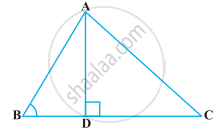
आकृति में AD त्रिभुज ABC की एक माध्यिका है तथा AM ⊥ BC है। सिद्ध कीजिए कि
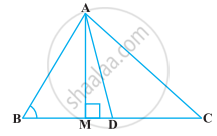
(i) AC2 = AD2 + BC.DM + `("BC"/2)^2`
(ii) AB2 = AD2 – BC.DM + `("BC"/2)^2`
(ii) AC2 + AB2 = 2AD2 + `1/2` BC2
आकृति में, रेखाखंड DF त्रिभुज ABC की भुजा AC को बिंदु E पर इस प्रकार प्रतिच्छेद करता है कि E, भुजा AC का मध्य-बिंदु है और ∠AEF = ∠AFE है। सिद्ध कीजिए कि `(BD)/(CD) = (BF)/(CE)` है।

