Advertisements
Advertisements
प्रश्न
सिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण पर खींचे गए अर्धवृत्त का क्षेत्रफल अन्य दो भुजाओं पर खींचे गए अर्धवृत्तों के क्षेत्रफलों के योग के बराबर होता है।
उत्तर
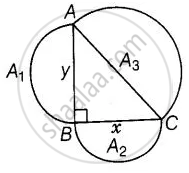
मान लीजिए ABC एक समकोण त्रिभुज है, जिसका कोण B समकोण है और AB = y, BC = x है।
भुजाओं AB, BC और AC पर क्रमशः व्यास AB, BC और AC के साथ तीन अर्धवृत्त खींचे गए हैं।
पुनः माना AB, BC और AC व्यास वाले वृत्तों का क्षेत्रफल क्रमशः A1, A2 और A3 है।
साबित करने के लिए: A3 = A1 + A2
प्रमाण: ΔABC में,
पाइथागोरस प्रमेय द्वारा,
AC2 = AB2 + BC2
⇒ AC2 = y2 + x2
⇒ AC = `sqrt(y^2 + x^2)`
हम जानते हैं कि,
त्रिज्या वाले अर्धवृत्त का क्षेत्रफल,
r = `(pir^2)/2`
∴ AC पर खींचे गए अर्धवृत्त का क्षेत्रफल,
A3 = `pi/2(("AC")/2)^2`
= `pi/2(sqrt(y^2 + x^2)/2)^2`
⇒ A3 = `(pi(y^2 + x^2))/8` ...(i)
अब, AB पर खींचे गए अर्धवृत्त का क्षेत्रफल,
A1 = `pi/2 (("AB")/2)^2`
⇒ A1 = `pi/2(y/2)^2`
⇒ A1 = `(piy^2)/8` ...(ii)
और BC पर बनाये गये अर्धवृत्त का क्षेत्रफल,
A2 = `pi/2(("BC")/2)^2`
= `pi/2(x/2)^2`
⇒ A2 = `(pix^2)/8`
समीकरण (ii) और (iii) को जोड़ने पर, हम पाते हैं।
A1 + A2 = `(piy^2)/8 + (pix^2)/8`
= `(pi(y^2 + x^2))/8`
= A3 ...[समीकरण (i) से]
⇒ A1 + A2 = A3
अतः सिद्ध हुआ।
APPEARS IN
संबंधित प्रश्न
ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है। सिद्ध कीजिए कि AB2 = 2AC2 है।
ABC एक समद्विबाहु त्रिभुज है जिसमें AC = BC है। यदि AB2 = 2AC2 है, तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है।
एक हवाई जहाज एक हवाई अड्डे से उत्तर की ओर 1000 km/hr की चाल से उड़ता है। इसी समय एक अन्य हवाई जहाज उसी हवाई अड्डे से पश्चिम की ओर 1200 km/hr की चाल से उड़ता है। `1 1/2` घंटे के बाद दोनों हवाई जहाजों के बीच की दूरी कितनी होगी?
आकृति में ABC एक त्रिभुज है जिसमें ∠ABC > 90° हैं तथा AD ⊥ CB है। सिद्ध कीजिए कि AC2 = AB2 + BC2 + 2 BC.BD है।
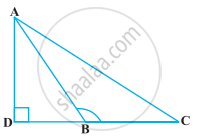
आकृति में ABC एक त्रिभुज है जिसमें ∠ABC < 90° हैं तथा AD ⊥ BC है। सिद्ध कीजिए कि AC2 = AB2 + BC2 – 2BC.BD है।
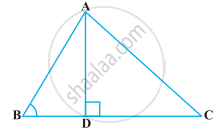
10 m लंबी एक सीढ़ी, जो एक उर्ध्वाधर दीवार के सहारे टिकी हुई है, के निचले सिरे की दीवार के आधार से दूरी 6 m है। दीवार पर उस बिंदु की ऊँचाई ज्ञात कीजिए, जहाँ तक सीढ़ी का ऊपरी सिरा पहुँचता है।
5 m लंबी एक सीढ़ी एक ऊर्ध्वाधर दीवार के सहारे इस प्रकार टिकी हुई है कि उसका ऊपरी सिरा दीवार पर 4 m ऊँचे बिंदु तक पहुँचता है। यदि सीढ़ी के निचले सिरे को दीवार की ओर 1.6 m खिसकाया जाए, तो वह दूरी ज्ञात कीजिए जो सीढ़ी का ऊपरी सिरा ऊपर की ओर दीवार पर सरक जाएगा।
एक समलंब ABCD, जिसमें AB || DC है, के विकर्णों AC और BD का प्रतिच्छेद बिंदु O है। O से होकर एक रेखाखंड PQ भुजा AB के समांतर खींचा गया है, जो AD को P और BC को Q पर मिलता है। सिद्ध कीजिए कि PO = QO है।
आकृति में, रेखाखंड DF त्रिभुज ABC की भुजा AC को बिंदु E पर इस प्रकार प्रतिच्छेद करता है कि E, भुजा AC का मध्य-बिंदु है और ∠AEF = ∠AFE है। सिद्ध कीजिए कि `(BD)/(CD) = (BF)/(CE)` है।

सिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण पर खींचे गए समबाहु त्रिभुज का क्षेत्रफल अन्य दो भुजाओं पर खींचे गए समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होता है।
