Advertisements
Advertisements
प्रश्न
आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि
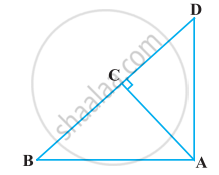
AD2 = BD.CD
उत्तर
समकोण त्रिभुज ABD में समकोण बनाने वाले शीर्ष A से BD पर लम्ब AC डाला गया है।
∆ACB ∼ ∆DCA ∼ ∆DAB …(1) [प्रमेय 6.7 से]
∆DCA ∼ ∆DAB [समीकरण (1) से]
⇒ `"AD"/"BD" = "CD"/"AD"` [समरूप त्रिभुजों के प्रगुण]
⇒ AD2 = BD.CD
इति सिद्धम्
APPEARS IN
संबंधित प्रश्न
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
3 cm, 8 cm, 6 cm
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
50 cm, 80 cm, 100 cm
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
13 cm, 12 cm, 5 cm
10 m लंबी एक सीढ़ी एक दीवार पर टिकाने पर भूमि से 8 m की ऊँचाई पर स्थित एक खिड़की तक पहुँचती है। दीवार के आधार से सीढ़ी के निचले सिरे की दूरी ज्ञात कीजिए।
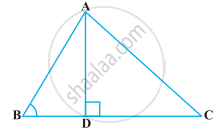
आकृति में ABC एक त्रिभुज है जिसमें ∠ABC < 90° हैं तथा AD ⊥ BC है। सिद्ध कीजिए कि AC2 = AB2 + BC2 – 2BC.BD है।
आकृति में AD त्रिभुज ABC की एक माध्यिका है तथा AM ⊥ BC है। सिद्ध कीजिए कि
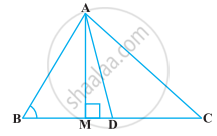
(i) AC2 = AD2 + BC.DM + `("BC"/2)^2`
(ii) AB2 = AD2 – BC.DM + `("BC"/2)^2`
(ii) AC2 + AB2 = 2AD2 + `1/2` BC2
क्या भुजाओं 25 cm, 5 cm और 24 cm वाला त्रिभुज एक समकोण त्रिभुज है? अपने उत्तर के लिए कारण दीजिए।
भुजा 8 cm वाले एक समबाहु त्रिभुज का शीर्षलंब ज्ञात कीजिए।
शहर A से शहर B तक जाने के लिए एक मार्ग शहर C से होकर इस प्रकार जाता है कि AC ⊥ CB है, AC = 2x km और CB = 2(x + 7) km है। दोनों शहरों A और B को सीधा जोड़ने के लिए, एक 26 km लंबे राजमार्ग बनाने की एक योजना है। ज्ञात कीजिए कि राजमार्ग बन जाने के बाद, शहर A से शहर B तक जाने में कितनी दूरी कम चलनी पड़ेगी।
∆PQR में, PD ⊥ QR इस प्रकार है कि D भुजा QR पर स्थित है। यदि PQ = a, PR = b, QD = c और DR = d है, तो सिद्ध कीजिए कि (a + b)(a – b) = (c + d)(c – d) है।
