Advertisements
Advertisements
प्रश्न
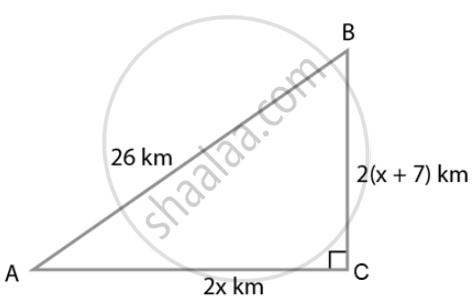
शहर A से शहर B तक जाने के लिए एक मार्ग शहर C से होकर इस प्रकार जाता है कि AC ⊥ CB है, AC = 2x km और CB = 2(x + 7) km है। दोनों शहरों A और B को सीधा जोड़ने के लिए, एक 26 km लंबे राजमार्ग बनाने की एक योजना है। ज्ञात कीजिए कि राजमार्ग बन जाने के बाद, शहर A से शहर B तक जाने में कितनी दूरी कम चलनी पड़ेगी।
उत्तर
प्रश्न के अनुसार,
AC ⊥ CB,
AC = 2x km,
CB = 2(x + 7) km
और AB = 26 km
इस प्रकार, हमें C पर समकोण ∆ACB प्राप्त होता है।
अब, ∆ACB से,
पाइथागोरस प्रमेय का उपयोग करते हुए,
AB2 = AC2 + BC2
⇒ (26)2 = (2x)2 + {2(x + 7)}2
⇒ 676 = 4x2 + 4(x2 + 196 + 14x)
⇒ 676 = 4x2 + 4x2 + 196 + 56x
⇒ 676 = 82 + 56x + 196
⇒ 8x2 + 56x – 480 = 0
समीकरण को 8 से विभाजित करने पर, हमें प्राप्त होता है,
x2 + 7x – 60 = 0
x2 + 12x – 5x – 60 = 0
x(x + 12) – 5(x + 12) = 0
(x + 12)(x – 5) = 0
∴ x = –12 or x = 5
चूंकि दूरी ऋणात्मक नहीं हो सकती, इसलिए हम x = –12 की उपेक्षा करते हैं।
∴ x = 5
अब,
AC = 2x = 10 km
BC = 2(x + 7)
= 2(5 + 7)
= 24 km
इस प्रकार, शहर A से शहर C के माध्यम से शहर B तक तय की गई दूरी = AC + BC
AC + BC = 10 + 24
= 34 km
राजमार्ग बनने के बाद शहर A से शहर B तक तय की गई दूरी = BA = 26 km
इसलिए, दूरी बचाई = 34 – 26 = 8 km.
APPEARS IN
संबंधित प्रश्न
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
7 cm, 24 cm, 25 cm
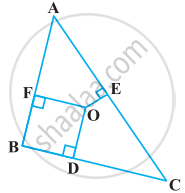
आकृति में ∆ABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD ⊥ BC, OE ⊥ AC और OF ⊥ AB है। दर्शाइए कि
- OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
- AF2 + OB2 + CE2 = AE2 + CD2 + BF2
10 m लंबी एक सीढ़ी एक दीवार पर टिकाने पर भूमि से 8 m की ऊँचाई पर स्थित एक खिड़की तक पहुँचती है। दीवार के आधार से सीढ़ी के निचले सिरे की दूरी ज्ञात कीजिए।
एक हवाई जहाज एक हवाई अड्डे से उत्तर की ओर 1000 km/hr की चाल से उड़ता है। इसी समय एक अन्य हवाई जहाज उसी हवाई अड्डे से पश्चिम की ओर 1200 km/hr की चाल से उड़ता है। `1 1/2` घंटे के बाद दोनों हवाई जहाजों के बीच की दूरी कितनी होगी?
दो खंभे जिनकी ऊँचाइयाँ 6 m और 11 m हैं तथा ये समतल भूमि पर खड़े हैं। यदि इनके पाद बिंदुओं के बीच की दूरी 12 m है तो इनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।
किसी समबाहु त्रिभुज में, सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्षलंब के वर्ग के चार गुने के बराबर होता है।
∆PQR में, PD ⊥ QR इस प्रकार है कि D भुजा QR पर स्थित है। यदि PQ = a, PR = b, QD = c और DR = d है, तो सिद्ध कीजिए कि (a + b)(a – b) = (c + d)(c – d) है।
एक समलंब ABCD, जिसमें AB || DC है, के विकर्णों AC और BD का प्रतिच्छेद बिंदु O है। O से होकर एक रेखाखंड PQ भुजा AB के समांतर खींचा गया है, जो AD को P और BC को Q पर मिलता है। सिद्ध कीजिए कि PO = QO है।
आकृति में, रेखाखंड DF त्रिभुज ABC की भुजा AC को बिंदु E पर इस प्रकार प्रतिच्छेद करता है कि E, भुजा AC का मध्य-बिंदु है और ∠AEF = ∠AFE है। सिद्ध कीजिए कि `(BD)/(CD) = (BF)/(CE)` है।

सिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण पर खींचे गए अर्धवृत्त का क्षेत्रफल अन्य दो भुजाओं पर खींचे गए अर्धवृत्तों के क्षेत्रफलों के योग के बराबर होता है।
