Advertisements
Advertisements
प्रश्न
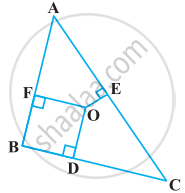
आकृति में ∆ABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD ⊥ BC, OE ⊥ AC और OF ⊥ AB है। दर्शाइए कि
- OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
- AF2 + OB2 + CE2 = AE2 + CD2 + BF2
उत्तर
दिया है: ∆ABC के अभ्यंतर में स्थित कोई बिन्दु O तथा
OD ⊥ BC, OE ⊥ CA, OF ⊥ AB
रचना: OA, OB और OC को मिलाइए।
(i) ∵ पाइथागोरस प्रमेय से,
समकोण ∆OFA में,
OA2 – OF2 = AF2 …(1)
समकोण ∆ODB में,
OB2 – OD2 = BD2 ….(2)
एवं समकोण ∆OEC में,
OC2 – OE2 = CE2 …(3)
OA2 – OF2 + OB2 – OD2 + OC2 – OE2 = AF2 + BD2 + CE2
[समीकरण (1) + (2) + (3) से]
OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2 …(4)
इति सिद्धम्
(ii) चूँकि पाइथागोरस प्रमेय से,
समकोण ∆OEA में,
OA2 – OE2 = AE2 ….(5)
समकोण ∆OFB में,
OB2 – OF2 = BF2 ….(6)
एवं समकोण ∆ODC में,
OC2 – OD2 = CD2 ….(7)
OA2 – OE2 + OB2 – OF2 + OC2 – OD2 = AE2 + BF2 + CD2
[समीकरण (5) + (6) + (7) से]
OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AE2 + CD2 + BF2 …(8)
AF2 + BD2 + CE2 = AE2 + CD2 + BF2
[समीकरण (4) एवं (8) से]
इति सिद्धम्
APPEARS IN
संबंधित प्रश्न
ABC एक समद्विबाहु त्रिभुज है जिसमें AC = BC है। यदि AB2 = 2AC2 है, तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है।
एक समबाहु त्रिभुज ABC की भुजा 2a है। उसके प्रत्येक शीर्षलंब की लंबाई ज्ञात कीजिए।
18 m ऊंचे एक ऊर्ध्वाधर खंभे के ऊपरी सिरे से एक तार का एक सिरा जुड़ा हुआ है तथा तार का दूसरा सिरा एक खूँटे से जुड़ा हुआ है। खंभे के आधार से खूँटे को कितनी दूरी पर गाड़ा जाए कि तार तना रहे जबकि तार की लंबाई 24 m है।
दो खंभे जिनकी ऊँचाइयाँ 6 m और 11 m हैं तथा ये समतल भूमि पर खड़े हैं। यदि इनके पाद बिंदुओं के बीच की दूरी 12 m है तो इनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।
आकृति में AD त्रिभुज ABC की एक माध्यिका है तथा AM ⊥ BC है। सिद्ध कीजिए कि
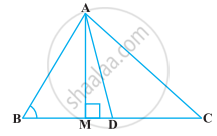
(i) AC2 = AD2 + BC.DM + `("BC"/2)^2`
(ii) AB2 = AD2 – BC.DM + `("BC"/2)^2`
(ii) AC2 + AB2 = 2AD2 + `1/2` BC2
भुजा 8 cm वाले एक समबाहु त्रिभुज का शीर्षलंब ज्ञात कीजिए।
10 m लंबी एक सीढ़ी, जो एक उर्ध्वाधर दीवार के सहारे टिकी हुई है, के निचले सिरे की दीवार के आधार से दूरी 6 m है। दीवार पर उस बिंदु की ऊँचाई ज्ञात कीजिए, जहाँ तक सीढ़ी का ऊपरी सिरा पहुँचता है।
5 m लंबी एक सीढ़ी एक ऊर्ध्वाधर दीवार के सहारे इस प्रकार टिकी हुई है कि उसका ऊपरी सिरा दीवार पर 4 m ऊँचे बिंदु तक पहुँचता है। यदि सीढ़ी के निचले सिरे को दीवार की ओर 1.6 m खिसकाया जाए, तो वह दूरी ज्ञात कीजिए जो सीढ़ी का ऊपरी सिरा ऊपर की ओर दीवार पर सरक जाएगा।
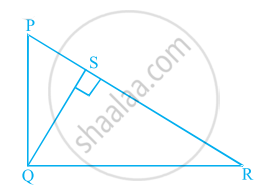
आकृति में PQR एक समकोण त्रिभुज है, जिसका ∠Q समकोण है तथा QS ⊥ PR है। यदि PQ = 6 cm और PS = 4 cm है, तो QS, RS और QR ज्ञात कीजिए।
आकृति में, रेखाखंड DF त्रिभुज ABC की भुजा AC को बिंदु E पर इस प्रकार प्रतिच्छेद करता है कि E, भुजा AC का मध्य-बिंदु है और ∠AEF = ∠AFE है। सिद्ध कीजिए कि `(BD)/(CD) = (BF)/(CE)` है।

