Advertisements
Advertisements
प्रश्न
एक समबाहु त्रिभुज ABC की भुजा 2a है। उसके प्रत्येक शीर्षलंब की लंबाई ज्ञात कीजिए।
उत्तर
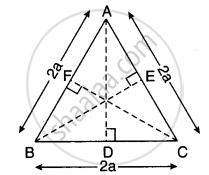
∆ABC एक समबाहु त्रिभुज है जिसमें AB = BC = CA = 2a
हम जानते हैं कि समबाहु त्रिभुजों के शीर्षलंब परस्पर बराबर होते हैं तथा सम्मुख भुजाओं को समद्विभाजित करते हैं। समकोण त्रिभुज
ADB में ∠D समकोण है [AD ⊥ BC]
तथा कर्ण AB = 2a [दिया है]
BD = a [BD = DC]
अब समकोण ∆ADB में ∠ADB समकोण है।
⇒ AD2 = AB2 – BD2 [पाइथागोरस प्रमेय से]
⇒ AD2 = (2a)2 – (a)2
⇒ AD2 = 4a2 – a2 = 3a2
⇒ AD = `sqrt3a^2 = asqrt3`
अतः दिए हुए समबाहु को प्रत्येक शीर्षलंब की लंबाई `asqrt3` है।
APPEARS IN
संबंधित प्रश्न
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
50 cm, 80 cm, 100 cm
आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि
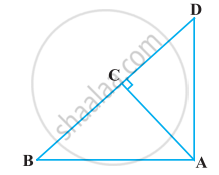
AC2 = BC.DC
आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि

AD2 = BD.CD
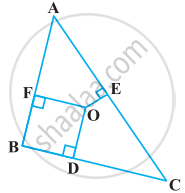
आकृति में ∆ABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD ⊥ BC, OE ⊥ AC और OF ⊥ AB है। दर्शाइए कि
- OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
- AF2 + OB2 + CE2 = AE2 + CD2 + BF2
किसी समबाहु त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि BD = `1/3` BC है। सिद्ध कीजिए कि 9AD2 = 7AB2 है।
भुजा 8 cm वाले एक समबाहु त्रिभुज का शीर्षलंब ज्ञात कीजिए।
शहर A से शहर B तक जाने के लिए एक मार्ग शहर C से होकर इस प्रकार जाता है कि AC ⊥ CB है, AC = 2x km और CB = 2(x + 7) km है। दोनों शहरों A और B को सीधा जोड़ने के लिए, एक 26 km लंबे राजमार्ग बनाने की एक योजना है। ज्ञात कीजिए कि राजमार्ग बन जाने के बाद, शहर A से शहर B तक जाने में कितनी दूरी कम चलनी पड़ेगी।
18 m ऊँचे एक ध्वज स्तंभ की छाया की लंबाई 9.6 m है। इस स्तंभ के ऊपरी सिरे की छाया के दूरस्थ सिरे से दूरी ज्ञात कीजिए।
किसी चतुर्भुज ABCD में, ∠A + ∠D = 90° है। सिद्ध कीजिए कि AC2 + BD2 = AD2 + BC2 है।
[संकेत : AB और DC को E पर मिलने के लिए बढ़ाइए]।
सिद्ध कीजिए कि एक समकोण त्रिभुज के कर्ण पर खींचे गए समबाहु त्रिभुज का क्षेत्रफल अन्य दो भुजाओं पर खींचे गए समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होता है।
