Advertisements
Advertisements
Question
आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि
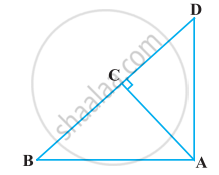
AC2 = BC.DC
Solution
समकोण त्रिभुज ABD में समकोण बनाने वाले शीर्ष A से BD पर लम्ब AC डाला गया है।
∆ACB ∼ ∆DCA ∼ ∆DAB …(1) [प्रमेय 6.7 से]
∆ACB ∼ ∆DCA [समीकरण (1) से]
⇒ `"AC"/"DC" = "BC"/"AC"` [समरूप त्रिभुजों के प्रगुण]
⇒ AC2 = BC.DC
इति सिद्धम्
APPEARS IN
RELATED QUESTIONS
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
7 cm, 24 cm, 25 cm
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
50 cm, 80 cm, 100 cm
आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि

AD2 = BD.CD
ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है। सिद्ध कीजिए कि AB2 = 2AC2 है।
दो खंभे जिनकी ऊँचाइयाँ 6 m और 11 m हैं तथा ये समतल भूमि पर खड़े हैं। यदि इनके पाद बिंदुओं के बीच की दूरी 12 m है तो इनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।
सही उत्तर चुनकर उसका औचित्य दीजिए: ∆ABC में, AB = `6sqrt3` cm, AC = 12 cm और BC = 6 cm है। कोण B है: ______
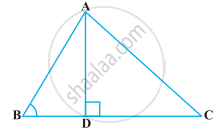
आकृति में ABC एक त्रिभुज है जिसमें ∠ABC < 90° हैं तथा AD ⊥ BC है। सिद्ध कीजिए कि AC2 = AB2 + BC2 – 2BC.BD है।
यदि ∆PQR की एक भुजा PQ पर S एक ऐसा बिंदु है कि PS = QS = RS है, तो ______।
भुजा 8 cm वाले एक समबाहु त्रिभुज का शीर्षलंब ज्ञात कीजिए।
एक समलंब ABCD, जिसमें AB || DC है, के विकर्णों AC और BD का प्रतिच्छेद बिंदु O है। O से होकर एक रेखाखंड PQ भुजा AB के समांतर खींचा गया है, जो AD को P और BC को Q पर मिलता है। सिद्ध कीजिए कि PO = QO है।
