Advertisements
Advertisements
Question
आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा AC ⊥ BD है। दर्शाइए कि
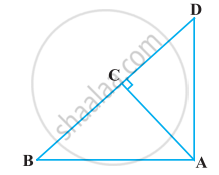
AB2 = BC.BD
Solution
समकोण त्रिभुज ABD में समकोण बनाने वाले शीर्ष A से BD पर लम्ब AC डाला गया है।
∆ACB ∼ ∆DCA ∼ ∆DAB …(1) [प्रमेय 6.7 से]
∆ACB ∼ ∆DAB [समीकरण (1) से]
⇒ `"AB"/"BD" = "BC"/"AB"` [समरूप त्रिभुजों के प्रगुण]
⇒ AB² = BC.BD
इति सिद्धम्
APPEARS IN
RELATED QUESTIONS
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
50 cm, 80 cm, 100 cm
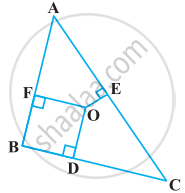
आकृति में ∆ABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD ⊥ BC, OE ⊥ AC और OF ⊥ AB है। दर्शाइए कि
- OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2
- AF2 + OB2 + CE2 = AE2 + CD2 + BF2
एक हवाई जहाज एक हवाई अड्डे से उत्तर की ओर 1000 km/hr की चाल से उड़ता है। इसी समय एक अन्य हवाई जहाज उसी हवाई अड्डे से पश्चिम की ओर 1200 km/hr की चाल से उड़ता है। `1 1/2` घंटे के बाद दोनों हवाई जहाजों के बीच की दूरी कितनी होगी?
एक त्रिभुज ABC जिसका कोण C समकोण है, की भुजाओं CA और CB पर क्रमशः बिंदु D और E स्थित हैं। सिद्ध कीजिए कि AE2 + BD2 = AB2 + DE2 है।
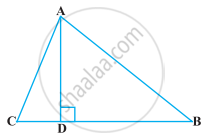
किसी त्रिभुज ABC के शीर्ष A से BC पर डाला गया लम्ब BC को बिंदु D पर इस प्रकार प्रतिच्छेद करता है कि DB = 3CD है (देखिए आकृति) सिद्ध कीजिए कि 2AB2 = 2AC2 + BC2 है।
किसी समबाहु त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि BD = `1/3` BC है। सिद्ध कीजिए कि 9AD2 = 7AB2 है।
सही उत्तर चुनकर उसका औचित्य दीजिए: ∆ABC में, AB = `6sqrt3` cm, AC = 12 cm और BC = 6 cm है। कोण B है: ______
क्या भुजाओं 25 cm, 5 cm और 24 cm वाला त्रिभुज एक समकोण त्रिभुज है? अपने उत्तर के लिए कारण दीजिए।
18 m ऊँचे एक ध्वज स्तंभ की छाया की लंबाई 9.6 m है। इस स्तंभ के ऊपरी सिरे की छाया के दूरस्थ सिरे से दूरी ज्ञात कीजिए।
किसी चतुर्भुज ABCD में, ∠A + ∠D = 90° है। सिद्ध कीजिए कि AC2 + BD2 = AD2 + BC2 है।
[संकेत : AB और DC को E पर मिलने के लिए बढ़ाइए]।
