Advertisements
Advertisements
प्रश्न
आकृति में ∠DFE = 90°, रेख FG ⊥ रेख ED. यदि GD = 8, FG = 12, तो (1) EG (2) FD (3) EF का मान ज्ञात कीजिए।

उत्तर
(i) ΔDEF में,
∠DFE = 90° ..............(दिया है)
रेख FG ⊥ कर्ण DE ...............(दिया है)
∴ ज्यामितीय माध्य के गुणधर्म से,
FG2 = DG × EG
∴ 122 = 8 × EG
∴ EG = `(12 xx 12)/8`
∴ EG = 18.
(ii) ΔDGF में, ∠DGF = 90° ..............(दिया है)
∴ पायथागोरस के प्रमेय से,
FD2 = DG2 + GF2
∴ FD2 = 82 + 122
∴ FD2 = 64 + 144
FD2 = 208
∴ FD = `4sqrt13`. ........(दोनों पक्षों का वर्गमूल लेने पर)
(iii) ΔEGF में, ∠EGF = 90° ..............(दिया है)
∴ पायथागोरस के प्रमेय से,
EF2 = EG2 + GF2
∴ EF2 = 182 + 122
EF2 = 324 + 144
EF2 = 468
∴ EF = `6sqrt13` ....................(दोनों पक्षों का वर्गमूल लेने पर)
∴ EG = 18, FD = `underline(4sqrt13)` और EF = `underline(6sqrt13)`.
APPEARS IN
संबंधित प्रश्न
किसी आयत की लंबाई 35 सेमी तथा चौड़ाई 12 सेमी हो तो उस आयत के विकर्ण की लंबाई ज्ञात कीजिए।
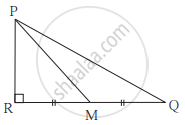
आकृति में M यह भुजा QR का मध्यबिंदु है। ∠PRQ = 90° तो सिद्ध कीजिए कि, PQ2 = 4PM2 - 3PR2
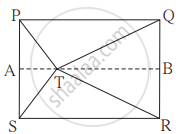
आकृति में दर्शाएनुसार बिंदु T यह आयत PQRS के अंतर्भाग में स्थित है। तो सिद्ध कीजिए कि, TS2 + TQ2 = TP2 + TR2 (आकृति में दर्शाएअनुसार रेख AB || भुजा SR ऐसा खींचिए कि A-T-B)
निम्नलिखित बहुवैकल्पिक प्रश्न के दिए गए उत्तरों में से उचित विकल्प चुनकर लिखिए।
समकोण त्रिभुज में समकोण बनानेवाली भुजाओं के वर्गों का योगफल 169 हो तो उसके कर्ण की लंबाई कितनी होगी?
किसी आयत की भुजाएँ क्रमश: 11 सेमी तथा 60 सेमी हों तो उसके विकर्ण की लंबाई ज्ञात कीजिए।
किसी समकोण त्रिभुज में समकोण बनाने वाली भुजाएँ क्रमश: 9 सेमी तथा 12 सेमी हों तो उस त्रिभुज के कर्ण की लंबाई ज्ञात कीजिए।
किसी आयत का क्षेत्रफल 192 वर्ग सेमी तथा उसकी लंबाई 16 सेमी हो, तो उस आयत के विकर्ण की लंबाई ज्ञात कीजिए।
किसी समबाहु त्रिभुज की ऊँचाई `sqrt3` सेमी हो, तो उस त्रिभुज के भुजा की लंबाई तथा उसकी परिमिति ज्ञात कीजिए।
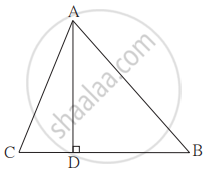
ΔABC में रेख AD ⊥ रेख BC और DB = 3CD, तो सिद्ध कीजिए कि : 2AB2 = 2AC2 + BC2
यदि a, b, c त्रिभुज की भुजाएँ हैं और a2 + b2 = c2 हो, तो उस त्रिभुज के प्रकार का नाम लिखिए?
