Question

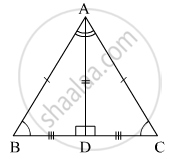
ΔABC मध्ये ∠BAC चा दुभाजक बाजू BC वर लंब असेल तर सिद्ध करा की ΔABC हा समद्‌विभुज त्रिकोण आहे.

Answer 1

पक्ष: रेख AD हा ∠BAC चा दुभाजक आहे. रेख AD ⊥ रेख BC.

साध्य: ΔABC हा समद्‌विभुज त्रिकोण आहे.

सिद्धता:

∆ABD व ∆ACD मध्ये,

∠BAD ≅ ∠CAD   ...(रेख AD हा ∠BAC चा दुभाजक आहे.)

seg AD ≅ seg AD   ...(सामाईक बाजू)

∠ADB ≅ ∠ADC   ...(प्रत्येक कोन 90° आहे)

∴ ∆ABD ≅ ∆ACD   ...(कोबाको कसोटी)

∴ seg AB ≅ seg AC  ...(एकरूप त्रिकोणाच्या संगत बाजू)

∴ ∆ABC हा समद्‌विभुज त्रिकोण आहे.