Balbharati solutions for Geometry (Mathematics 2) [Marathi] 9 Standard Maharashtra State Board chapter 3 - त्रिकोण [Latest edition]

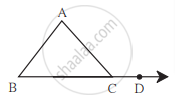
आकृती मध्ये ΔABC चा ∠ACD हा बाह्यकोन आहे. ∠B = 40°, ∠A = 70° तर m∠ACD काढा.

ΔPQR मध्ये ∠P = 70°, ∠Q = 65° तर ∠R चे माप काढा.

त्रिकोणाच्या कोनांची मापे x°, (x - 20)°, (x - 40)° असतील तर प्रत्येक कोनाचे माप किती?

त्रिकोणाच्या तीन कोनांपैकी एक कोन सर्वांत लहान कोनाच्या दुप्पट व दुसरा कोन सर्वांत लहान कोनाच्या तिप्पट आहे तर त्या तिन्ही कोनांची मापे काढा.

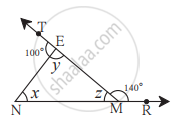
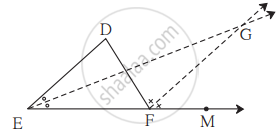
आकृती मध्ये दिलेल्या कोनांच्या मापांवरून x, y, z च्या किमती काढा.

खाली दिलेले आकृती मध्ये रेषा AB || रेषा DE आहे. दिलेल्या मापांवरून ∠DRE व ∠ARE ची मापे काढा.

ΔABC मध्ये ∠A  व ∠B चे दुभाजक बिंदू O मध्ये छेदतात. जर ∠C = 70° तर ∠AOB चे माप काढा.

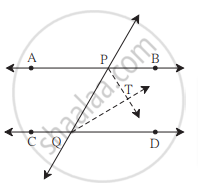
खाली दिलेले आकृती मध्ये रेषा AB || रेषा CD आणि रेषा PQ ही त्यांची छेदिका आहे. किरण PT आणि किरण QT हे अनुक्रमे ∠BPQ व ∠PQD चे दुभाजक आहेत, तर सिद्ध करा की ∠PTQ = 90°

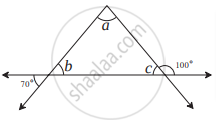
खालील आकृती मध्ये दिलेल्या माहितीवरून ∠a, ∠b व ∠c यांची मापे काढा.

खालील आकृती मध्ये रेख DE || रेख GF आहे. किरण EG व किरण FG हे अनुक्रमे ∠DEF व ∠DFM या कोनांचे दुभाजक आहेत. तर सिद्ध करा की,

1. ∠DEG = `1/2∠"EDF"`
2. EF = FG

पुढील उदाहरणातील त्रिकोणांच्या जोडीचे सारख्या खुणांनी दाखवलेले भाग एकरूप आहेत. त्‍यावरून दिलेल्या जोडीतील त्रिकोण ज्या कसोटीने एकरूप होतात ती कसोटी आकृतीखालील रिकाम्या जागेत लिहा.

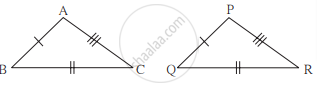
______ कसोटीने

ΔABC ≅ ΔPQR

पुढील उदाहरणातील त्रिकोणांच्या जोडीचे सारख्या खुणांनी दाखवलेले भाग एकरूप आहेत. त्‍यावरून दिलेल्या जोडीतील त्रिकोण ज्या कसोटीने एकरूप होतात ती कसोटी आकृतीखालील रिकाम्या जागेत लिहा.

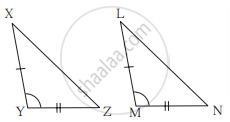
______ कसोटीने

ΔXYZ ≅ ΔLMN

पुढील उदाहरणातील त्रिकोणांच्या जोडीचे सारख्या खुणांनी दाखवलेले भाग एकरूप आहेत. त्‍यावरून दिलेल्या जोडीतील त्रिकोण ज्या कसोटीने एकरूप होतात ती कसोटी आकृतीखालील रिकाम्या जागेत लिहा.

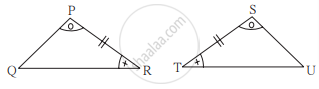
______ कसोटीने

ΔPRQ ≅ ΔSTU

पुढील उदाहरणातील त्रिकोणांच्या जोडीचे सारख्या खुणांनी दाखवलेले भाग एकरूप आहेत. त्‍यावरून दिलेल्या जोडीतील त्रिकोण ज्या कसोटीने एकरूप होतात ती कसोटी आकृतीखालील रिकाम्या जागेत लिहा.

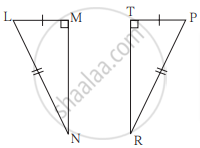
______ कसोटीने

ΔLMN ≅ ΔPTR

खालील त्रिकोणांच्या जोड्यांमध्ये दर्शवलेल्या माहितीचे निरीक्षण करा. ते त्रिकोण कोणत्या कसोटीनुसार एकरूप आहेत ते लिहा व त्यांचे उरलेले एकरूप घटक लिहा.

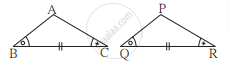
आकृतीत दर्शवलेल्या माहितीवरून,

ΔABC व ΔPQR मध्ये

∠ABC ≅ ∠PQR

रेख BC ≅ रेख QR

∠ACB ≅ ∠PRQ

∴ ΔABC ≅ ΔPQR        ...`square` कसोटी

∴ ∠BAC ≅ `square`            ...एकरूप त्रिकोणांचे संगत कोन.

रेख AB ≅ `square` आणि `square` ≅ रेख PR         ...एकरूप त्रिकोणांच्या संगत बाजू

खालील त्रिकोणांच्या जोड्यांमध्ये दर्शवलेल्या माहितीचे निरीक्षण करा. ते त्रिकोण कोणत्या कसोटीनुसार एकरूप आहेत ते लिहा व त्यांचे उरलेले एकरूप घटक लिहा.

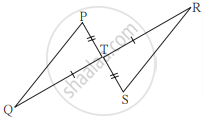
आकृतीत दर्शवलेल्या माहितीवरून,

ΔPTQ व ΔSTR मध्ये

रेख PT ≅ रेख ST

∠PTQ ≅ ∠STR     ...परस्पर विरुद्ध कोन

रेख TQ ≅ रेख TR

∴ ΔPTQ ≅ ΔSTR         ...`square` कसोटी

∴ `{:(∠"TPQ" ≅  square),(व  square ≅ ∠"TRS"):}}`      ...एकरूप त्रिकोणांचे संगत कोन.

रेख PQ ≅ `square`           ...एकरूप त्रिकोणांच्या संगत बाजू.

खालील आकृतीतील माहितीवरून ΔABC व ΔPQR या त्रिकोणांच्या एकरूपतेची कसोटी लिहून उरलेले एकरूप घटक लिहा.

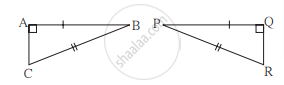
खालील आकृतीत दाखवल्याप्रमाणे ΔLMN व ΔPNM या त्रिकोणांमध्ये LM = PN, LN = PM आहे तर या त्रिकोणांच्या एकरूपतेची कसोटी लिहा व उरलेले एकरूप घटक लिहा.

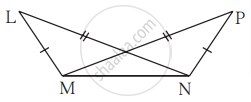
खालील आकृती मध्ये रेख AB ≅ रेख BC आणि रेख AD ≅ रेख CD. तर सिद्ध करा की, ΔABD ≅ ΔCBD

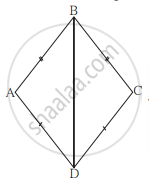
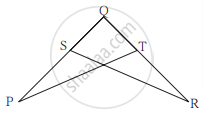
खालील आकृती मध्ये ∠P ≅ ∠R रेख PQ ≅ रेख QR तर सिद्ध करा की, ΔPQT ≅ ΔRQS

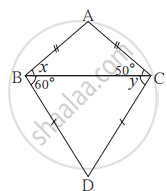
खालील आकृती मध्ये दाखवलेली माहिती पाहा. x आणि y च्या किंमती काढा. तसेच ∠ABD व ∠ACD ची मापे काढा.

काटकोन त्रिकोणात कर्णाची लांबी 15 असेल तर त्यावर काढलेल्या मध्यगेची लांबी काढा.

ΔPQR मध्ये ∠Q = 90°, PQ = 12, QR = 5 आणि QS ही PR ची मध्यगा असेल तर QS काढा.

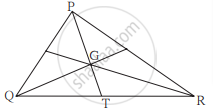
खालील आकृती मध्ये ΔPQR चा G हा मध्यगा संपात बिंदू आहे. जर GT = 2.5 सेमी, तर PG आणि PT यांची लांबी काढा.

खालील आकृती मध्ये, बिंदू A हा ∠XYZ च्या दुभाजकावर आहे. जर AX = 2 सेमी तर AZ काढा.

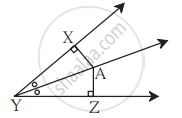
खालील आकृती मध्ये ∠RST = 56°, रेख PT ⊥ किरण ST, रेख PR ⊥ किरण SR आणि रेख PR ≅ रेख PT असेल तर ∠RSP काढा. कारण लिहा.

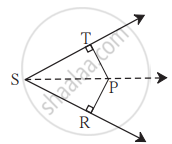
∆PQR मध्ये PQ = 10 सेमी, QR = 12 सेमी, PR = 8 सेमी तर या त्रिकोणाचा सर्वांत मोठा व सर्वांत लहान कोन ओळखा.

ΔFAN मध्ये ∠F = 80°, ∠A = 40° तर त्रिकोणाच्या सर्वात मोठ्या व सर्वांत लहान बाजूंची नावे सकारण लिहा.

सिद्ध करा की समभुज त्रिकोण समकोन त्रिकोण असतो.

ΔABC मध्ये ∠BAC चा दुभाजक बाजू BC वर लंब असेल तर सिद्ध करा की ΔABC हा समद्‌विभुज त्रिकोण आहे.

खालील आकृती मध्ये जर रेख PR ≅ रेख PQ तर दाखवा की रेख PS > रेख PQ.

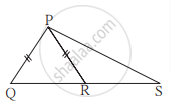
खालील आकृती मध्ये ΔABC चे रेख AD आणि रेख BE हे शिरोलंब आहेत आणि AE = BD आहे, तर सिद्ध करा की रेख AD ≅ रेख BE.

जर ΔXYZ ~ ΔLMN तर त्यांचे एकरूप असणारे संगत कोन लिहा आणि संगत बाजूंची गुणोत्तरे लिहा.

ΔXYZ मध्ये XY = 4 सेमी, YZ = 6 सेमी, XZ = 5 सेमी, जर ΔXYZ ~ ΔPQR आणि PQ = 8 सेमी असेल तर ΔPQR च्या उरलेल्या बाजू काढा.

समरूप त्रिकोणांच्या जोडीची कच्ची आकृती काढा. त्रिकोणांना नावे द्या. त्यांचे संगत कोन सारख्या खुणांनी दाखवा. त्रिकोणांच्या संगत बाजूंच्या लांबी प्रमाणात असलेल्या संख्यांनी दाखवा.

एका त्रिकोणाच्या दोन भुजा 5 सेमी व 1.5 सेमी असतील तर त्रिकाेणाच्या तिसऱ्या भुजेची लांबी ______ नसेल.

ΔPQR मध्ये जर ∠R > ∠Q तर ______ असेल.

ΔTPQ मध्ये ∠T = 65°, ∠P = 95° तर खालील विधानांपैकी सत्य विधान कोणते?

ΔABC हा समद्‌विभुज त्रिकोण आहे. ज्यात AB = AC आहे आणि BD व CE या दोन मध्यगा आहेत, तर BD = CE दाखवा.

ΔPQR मध्ये जर PQ > PR आणि ∠Q व ∠R चे दुभाजक S मध्ये छेदतात तर दाखवा की, SQ > SR.

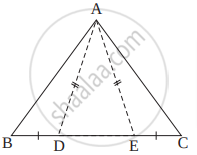
खालील आकृती मध्ये ΔABC च्या BC बाजू वर D आणि E बिंदू असे आहेत की BD = CE तसेच AD = AE तर दाखवा की, ΔABD ≅ ΔACE.

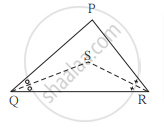
खालील आकृती मध्ये ΔPQR च्या बाजू QR वर S हा कोणताही एक बिंदू आहे तर सिद्ध करा की, PQ + QR + RP > 2PS

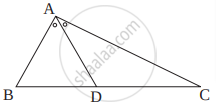
खालील आकृती मध्ये ΔABC च्या ∠BAC चा दुभाजक BC ला D बिंदूत छेदतो, तर सिद्ध करा की AB > BD.

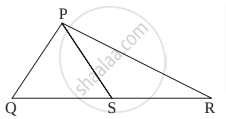
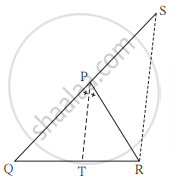
खालील आकृती मध्ये रेख PT हा ∠QPR चा दुभाजक आहे. बिंदू R मधून काढलेली रेख PT ला समांतर असणारी रेषा, किरण QP ला S बिंदूत छेदते, तर सिद्ध करा, PS = PR.

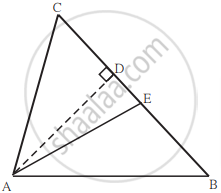
खालील आकृती मध्ये रेख AD ⊥ रेख BC. रेख AE हा ∠CAB चा दुभाजक असून E-D-C. तर दाखवा, की m∠DAE = `1/2` (m∠C - m∠B)