Advertisements
Advertisements
प्रश्न
खालील आकृती मध्ये ΔPQR च्या बाजू QR वर S हा कोणताही एक बिंदू आहे तर सिद्ध करा की, PQ + QR + RP > 2PS
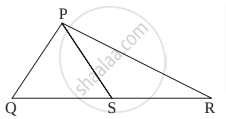
उत्तर
ΔPQS मध्ये,
PQ + QS > PS ...(i) (त्रिकोणाच्या कोणत्याही दोन बाजूंची बेरीज ही तिसऱ्या बाजूच्या लांबीपेक्षा जास्त असते.)
ΔPRS मध्ये,
RP + RS > PS ...(ii) (त्रिकोणाच्या कोणत्याही दोन बाजूंची बेरीज ही तिसऱ्या बाजूच्या लांबीपेक्षा जास्त असते.)
(i) आणि (ii) ची बेरीज करून
PQ + QS + RP + RS > PS + PS
∴ PQ + (QS + SR) + PR > 2PS
∴ PQ + QR + RP > 2PS ...(Q - S - R)
APPEARS IN
संबंधित प्रश्न
काटकोन त्रिकोणात कर्णाची लांबी 15 असेल तर त्यावर काढलेल्या मध्यगेची लांबी काढा.
ΔPQR मध्ये ∠Q = 90°, PQ = 12, QR = 5 आणि QS ही PR ची मध्यगा असेल तर QS काढा.
खालील आकृती मध्ये ΔPQR चा G हा मध्यगा संपात बिंदू आहे. जर GT = 2.5 सेमी, तर PG आणि PT यांची लांबी काढा.
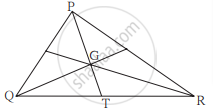
खालील आकृती मध्ये जर रेख PR ≅ रेख PQ तर दाखवा की रेख PS > रेख PQ.