Advertisements
Advertisements
प्रश्न
त्रिकोणाच्या कोनांची मापे x°, (x - 20)°, (x - 40)° असतील तर प्रत्येक कोनाचे माप किती?
उत्तर
त्रिकोणाच्या कोनांची मापे x°, (x - 20)°, (x - 40)°
∴ x° + (x - 20)° + (x - 40)° = 180° ...(त्रिकोणाच्या कोनांच्या मापांची बेरीज 180∘ असते.)
⇒ 3x - 60° = 180°
⇒ 3x = 180° + 60°
⇒ 3x = 240°
⇒ x° = `(240°)/3`
⇒ x° = 80°
∴ (x - 20)° = (80 - 20)° = 60°
∴ (x - 40)° = (80 - 40)° = 40°
∴ त्रिकोणाच्या कोनांची मापे 80°, 60° व 40° आहेत.
APPEARS IN
संबंधित प्रश्न
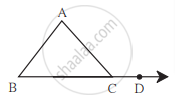
आकृती मध्ये ΔABC चा ∠ACD हा बाह्यकोन आहे. ∠B = 40°, ∠A = 70° तर m∠ACD काढा.
ΔPQR मध्ये ∠P = 70°, ∠Q = 65° तर ∠R चे माप काढा.
त्रिकोणाच्या तीन कोनांपैकी एक कोन सर्वांत लहान कोनाच्या दुप्पट व दुसरा कोन सर्वांत लहान कोनाच्या तिप्पट आहे तर त्या तिन्ही कोनांची मापे काढा.
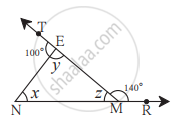
आकृती मध्ये दिलेल्या कोनांच्या मापांवरून x, y, z च्या किमती काढा.
खाली दिलेले आकृती मध्ये रेषा AB || रेषा DE आहे. दिलेल्या मापांवरून ∠DRE व ∠ARE ची मापे काढा.

ΔABC मध्ये ∠A व ∠B चे दुभाजक बिंदू O मध्ये छेदतात. जर ∠C = 70° तर ∠AOB चे माप काढा.
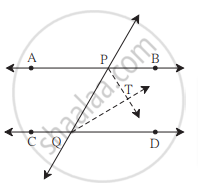
खाली दिलेले आकृती मध्ये रेषा AB || रेषा CD आणि रेषा PQ ही त्यांची छेदिका आहे. किरण PT आणि किरण QT हे अनुक्रमे ∠BPQ व ∠PQD चे दुभाजक आहेत, तर सिद्ध करा की ∠PTQ = 90°
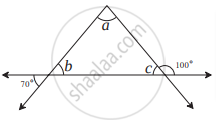
खालील आकृती मध्ये दिलेल्या माहितीवरून ∠a, ∠b व ∠c यांची मापे काढा.
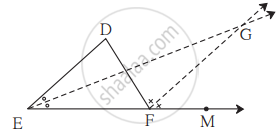
खालील आकृती मध्ये रेख DE || रेख GF आहे. किरण EG व किरण FG हे अनुक्रमे ∠DEF व ∠DFM या कोनांचे दुभाजक आहेत. तर सिद्ध करा की,
- ∠DEG = `1/2∠"EDF"`
- EF = FG