Advertisements
Advertisements
प्रश्न
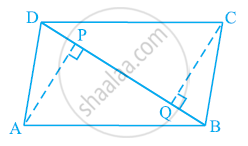
ABCD एक समांतर चतुर्भज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं (देखिए आकृति में)। दर्शाइए कि
- ΔAPB ≅ ΔCQD
- AP = CQ
उत्तर
i. ΔAPB और ΔCQD में,
∠APB = ∠CQD ...(प्रत्येक 90°)
AB = CD ...(समांतर चतुर्भुज ABCD की सम्मुख भुजाएँ)
∠ABP = ∠CDQ ...(AB || CD के लिए एकांतर अंत: कोण)
∴ ΔAPB ≅ ΔCQD ...(AAS सर्वांगसमता से)
ii. उपरोक्त परिणाम का उपयोग करके
ΔAPB ≅ ΔCQD, हम प्राप्त करते हैं
AP = CQ ...(CPCT से)
APPEARS IN
संबंधित प्रश्न
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
किसी समांतर चतुर्भुज के दो आसन्न कोणों का अनुपात 3 : 2 है। समांतर चतुर्भुज के सभी कोणों की माप ज्ञात कीजिए।
निम्नलिखित के लिए कारण दीजिए:
वर्ग, आयत, समांतर चतुर्भुज और समचतुर्भुज में से प्रत्येक एक चतुर्भुज भी है।
एक समांतर चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर प्रतिच्छेद करते हैं। यदि OA = 3 cm और OD = 2 cm है, तो AC और BD की लंबाई ज्ञात कीजिए।
∆ABC में, AB = 5 cm, BC = 8 cm और CA = 7 cm हैं। यदि D और E क्रमश : AB और BC के मध्य-बिंदु हैं, तो DE की लंबाई निर्धारित कीजिए।
ABCD एक समलंब है जिसमें AB || DC और ∠A = ∠B = 45° है। इस समलंब के कोण C और D ज्ञात कीजिए।
किसी समांतर चतुर्भुज के एक अधिक कोण वाले शीर्ष से खींचे गये दो शीर्षलंबों के बीच का कोण 30∘ है। उस अधिक कोण की माप है –
एक समांतर चतुर्भुज की आसन्न भुजाएँ 5 cm और 9 cm है। उसका परिमाप ______ है।
यदि एक चतुर्भुज के सम्मुख कोण बराबर हों, तो वह अवश्य ही समांतर चतुर्भुज होगा।
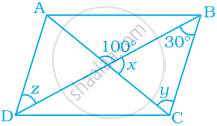
ABCD एक समांतर चतुर्भुज है। x, y और z के मान ज्ञात कीजिए।