Advertisements
Advertisements
प्रश्न
An ideal gas of density 1.7 × 10−3 g cm−3 at a pressure of 1.5 × 105 Pa is filled in a Kundt's tube. When the gas is resonated at a frequency of 3.0 kHz, nodes are formed at a separation of 6.0 cm. Calculate the molar heat capacities Cp and Cv of the gas.
उत्तर
Given:
Density of the ideal gas, ρ = 1.7 × 10−3 g/cm3
= 1.7 k/gm3
Pressure of the gas, P = 1.5 × 105 Pa
R = 8.3 J/mol-K
Resonance frequency of the gas = 3.0 kHz
Node separation in the Kundt's tube
`"l"/2 = 6 "cm"`
So, l = 2×6 = 12 cm = 12 × 10−2 m
So, V = fl = 3 × 103 × 12 × 10−2
= 360 m/s
Speed of sound, V =` sqrt( (gamma"p")/ρ)`
Or `"V"^2 =( gamma"p")/ρ `
`therefore gamma =("v"^2ρ)/"P" = ((360)^2 xx 1.7 xx 10^-3)/(1.5 xx 10^5)`
= 1.4688
Using `"C"_"P" -"C"_"v" = "R" and "C"_"p"/"C"_"v" = gamma`
We know that
`"C"_"v" = "R"/(gamma-1) =8.3/0.4688`
= 17.7 J / mol -K
Cp = R +Cv =8.3 +17.7 = 26 J /mol -K
APPEARS IN
संबंधित प्रश्न
Which of the following quantities is zero on an average for the molecules of an ideal gas in equilibrium?
Keeping the number of moles, volume and temperature the same, which of the following are the same for all ideal gases?
The average momentum of a molecule in a sample of an ideal gas depends on
Consider the quantity \[\frac{MkT}{pV}\] of an ideal gas where M is the mass of the gas. It depends on the
A rigid container of negligible heat capacity contains one mole of an ideal gas. The temperature of the gas increases by 1° C if 3.0 cal of heat is added to it. The gas may be
(a) helium
(b) argon
(c) oxygen
(d) carbon dioxide
A vessel containing one mole of a monatomic ideal gas (molecular weight = 20 g mol−1) is moving on a floor at a speed of 50 m s−1. The vessel is stopped suddenly. Assuming that the mechanical energy lost has gone into the internal energy of the gas, find the rise in its temperature.
The figure shows a cylindrical container containing oxygen (γ = 1.4) and closed by a 50-kg frictionless piston. The area of cross-section is 100 cm2, atmospheric pressure is 100 kPa and g is 10 m s−2. The cylinder is slowly heated for some time. Find the amount of heat supplied to the gas if the piston moves out through a distance of 20 cm.
An amount Q of heat is added to a monatomic ideal gas in a process in which the gas performs a work Q/2 on its surrounding. Find the molar heat capacity for the process
An ideal gas is taken through a process in which the pressure and the volume are changed according to the equation p = kV. Show that the molar heat capacity of the gas for the process is given by `"C" ="C"_"v" +"R"/2.`
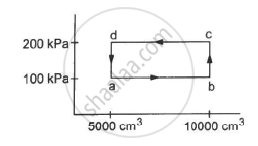
Half mole of an ideal gas (γ = 5/3) is taken through the cycle abcda, as shown in the figure. Take `"R" = 25/3"J""K"^-1 "mol"^-1 `. (a) Find the temperature of the gas in the states a, b, c and d. (b) Find the amount of heat supplied in the processes ab and bc. (c) Find the amount of heat liberated in the processes cd and da.
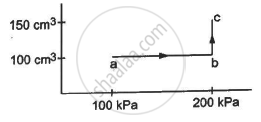
An ideal gas (γ = 1.67) is taken through the process abc shown in the figure. The temperature at point a is 300 K. Calculate (a) the temperatures at b and c (b) the work done in the process (c) the amount of heat supplied in the path ab and in the path bcand (d) the change in the internal energy of the gas in the process.
An ideal gas at pressure 2.5 × 105 Pa and temperature 300 K occupies 100 cc. It is adiabatically compressed to half its original volume. Calculate (a) the final pressure (b) the final temperature and (c) the work done by the gas in the process. Take γ = 1.5
Consider a given sample of an ideal gas (Cp/Cv = γ) having initial pressure p0 and volume V0. (a) The gas is isothermally taken to a pressure p0/2 and from there, adiabatically to a pressure p0/4. Find the final volume. (b) The gas is brought back to its initial state. It is adiabatically taken to a pressure p0/2 and from there, isothermally to a pressure p0/4. Find the final volume.
Figure shows a cylindrical tube with adiabatic walls and fitted with an adiabatic separator. The separator can be slid into the tube by an external mechanism. An ideal gas (γ = 1.5) is injected in the two sides at equal pressures and temperatures. The separator remains in equilibrium at the middle. It is now slid to a position where it divides the tube in the ratio 1 : 3. Find the ratio of the temperatures in the two parts of the vessel.

The figure shows an adiabatic cylindrical tube of volume V0 divided in two parts by a frictionless adiabatic separator. Initially, the separator is kept in the middle, an ideal gas at pressure p1 and temperature T1 is injected into the left part and another ideal gas at pressure p2 and temperature T2 is injected into the right part. Cp/Cv = γ is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the volumes of the two parts (b) the heat given to the gas in the left part and (c) the final common pressure of the gases.

In a diatomic molecule, the rotational energy at a given temperature ______.
- obeys Maxwell’s distribution.
- have the same value for all molecules.
- equals the translational kinetic energy for each molecule.
- is (2/3)rd the translational kinetic energy for each molecule.
The container shown in figure has two chambers, separated by a partition, of volumes V1 = 2.0 litre and V2 = 3.0 litre. The chambers contain µ1 = 4.0 and µ2 = 5.0 moles of a gas at pressures p1 = 1.00 atm and p2 = 2.00 atm. Calculate the pressure after the partition is removed and the mixture attains equilibrium.
| V1 | V2 |
| µ1, p1 | µ2 |
| p2 |
